АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение систем линейных уравнений матричным методом

Читайте также:
  1. A) к любой экономической системе
  2. A) прогрессивная система налогообложения.
  3. C) Систематическими
  4. CASE-технология создания информационных систем
  5. ERP и CRM система OpenERP
  6. HMI/SCADA – создание графического интерфейса в SCADА-системе Trace Mode 6 (часть 1).
  7. I СИСТЕМА, ИСТОЧНИКИ, ИСТОРИЧЕСКАЯ ТРАДИЦИЯ РИМСКОГО ПРАВА
  8. I. Основні риси політичної системи України
  9. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  10. I. Решение логических задач средствами алгебры логики
  11. I. Суспільство як соціальна система.
  12. I. Формирование системы военной психологии в России.

В инженерных расчетах довольно часто приходится решать системы линейных уравнений. В общем случае система имеет вид

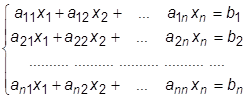(25.1)

Здесь х1, х2, …,хn – неизвестные параметры, значения которых необходимо найти; а11, а12, …, а1n, а21, …, а2n, …, аnn – известные коэффициенты при неизвестных параметрах х1, х2, …,хп. Первый индекс коэффициента означает номер строки (номер уравнения в системе), второй индекс – номер неизвестного параметра, при котором стоит данный коэффициент; b1, … bn – свободные члены в уравнениях, индекс означает номер уравнения.

Обычно число уравнений равно числу неизвестных. В этом случае коэффициенты при неизвестных и свободные члены образуют матрицу размером n ´ n +1. Здесь целесообразно свободные члены обозначить как элементы матрицы с индексами i,n+1 (аi,n+1). Параметр i принимает значения от 1 до n.

Для того, чтобы система имела единственное решение, входящие в нее n уравнений должны быть линейно независимыми, то есть никакое уравнение не может быть линейной комбинацией других уравнений. Необходимым и достаточным условием существования единственного решения является неравенство нулю определителя матрицы коэффициентов.

Алгоритмы решения задач такого типа делятся на прямые и итерационные. Прямые методы дают решения за конечное число действий. Для систем порядка n <200 применяются практически только прямые методы. Итерационные методы выгодны для систем со слабо заполненной матрицей большого порядка n @103-105.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)