Производные от неявных функций

Начнем с неявной функции одного переменного. Мы уже решали задачу о дифференцировании неявной функции одного переменного, но были рассмотрены лишь отдельные примеры. Сейчас же мы получим общую формулу, дающую производную от неявной функции одного переменного, и выясним условия существования этой производной.

Теорема. Пусть непрерывная неявная функция от задается уравнением:

где непрерывные функции в некоторой области содержащей точку координаты которой удовлетворяют уравнению кроме того, в этой точке Тогда функция от имеет производную:

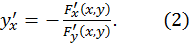
Доказательство. Пусть некоторому значению соответствует значение функции 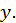При этом Дадим независимому переменному приращение 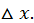Функция получит приращение т.е. значению аргумента соответствует значение функции В силу уравнения будем иметь:

Следовательно,

Левую часть последнего равенства, являющуюся полным приращением функции двух переменных, можно переписать так:

где и при и

Так как левая часть равна нулю, можно написать:

Разделим на и вычислим

Устремим к нулю. Тогда, учитывая, что при этом и также стремятся к нулю и что в пределе получим:

Пример. Уравнение определяет как неявную функцию от 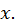Здесь

Следовательно,

Рассмотрим теперь уравнение вида:

Если паре чисел из некоторой области соответствует одно или несколько значений 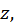удовлетворяющих уравнению 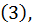то это уравнение неявно определяет одну или несколько однозначных функций 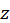от и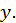

Найдем частные производные 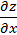и неявной функции 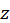от и 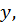определяемой уравнением 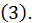Когда мы ищем мы считаем постоянным, поэтому здесь применима формула если только независимым переменным считать а функцией

Следовательно, Аналогично

Предполагается, что

Аналогичным образом определяются неявные функции любого числа переменных и находятся их частные производные.

Поиск по сайту: