 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интегрирование биномиальных дифференциалов
Биномиальным дифференциалом (или дифференциальным биномом) называют выражение вида  где
где  и
и 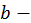 любые постоянные, а показатели степеней
любые постоянные, а показатели степеней  и
и  некоторые рациональные числа. Изучим вопрос об интегрируемости в элементарных функциях биномиальных дифференциалов. Отметим три случая, когда интеграл от биномиального дифференциала допускает рационализирующую подстановку.
некоторые рациональные числа. Изучим вопрос об интегрируемости в элементарных функциях биномиальных дифференциалов. Отметим три случая, когда интеграл от биномиального дифференциала допускает рационализирующую подстановку.
1.  целое число. В этом случае биномиальный дифференциал представляет собой иррациональность вида
целое число. В этом случае биномиальный дифференциал представляет собой иррациональность вида 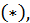 рассмотренную выше. Если через
рассмотренную выше. Если через  обозначить общий знаменатель дробей
обозначить общий знаменатель дробей 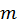 и
и 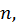 то интеграл от биномиального дифференциала в этом случае рационализируется подстановкой
то интеграл от биномиального дифференциала в этом случае рационализируется подстановкой 
2. 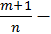 целое число. В этом случае, сделав подстановку
целое число. В этом случае, сделав подстановку

будем иметь 
Таким образом, если 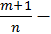 целое число, то получили иррациональность вида
целое число, то получили иррациональность вида 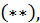 рассмотренную выше. Если через
рассмотренную выше. Если через 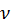 обозначить знаменатель рационального числа
обозначить знаменатель рационального числа 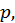 то правая часть выражения
то правая часть выражения 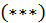 рационализируется подстановкой
рационализируется подстановкой 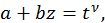 следовательно, интеграл от биномиального дифференциала в этом случае рационализируется подстановкой
следовательно, интеграл от биномиального дифференциала в этом случае рационализируется подстановкой 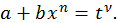
3. 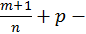 целое число. Интеграл
целое число. Интеграл 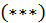 перепишем еще так:
перепишем еще так:
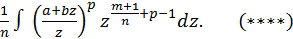
Таким образом, если 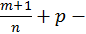 целое число, то получили снова иррациональность вида
целое число, то получили снова иррациональность вида  Если
Если 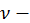 попрежнему знаменатель рационального числа
попрежнему знаменатель рационального числа 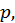 то интеграл
то интеграл  рационализируется подстановкой
рационализируется подстановкой 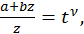 следовательно, интеграл от биномиального дифференциала в этом случае рационализируется подстановкой:
следовательно, интеграл от биномиального дифференциала в этом случае рационализируется подстановкой:
 Итак, интеграл от биномиального дифференциала допускает рационализирующую подстановку, если оказывается целым одно из чисел:
Итак, интеграл от биномиального дифференциала допускает рационализирующую подстановку, если оказывается целым одно из чисел: 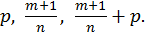
Эти случаи интегрируемости известны были еще Ньютону. Однако, лишь в середине XIX столетия Чебышев установил замечательный факт, что других случаев интегрируемости в элементарных функциях для биномиальных дифференциалов нет.
Пример. 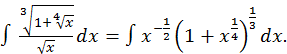
Здесь: 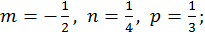 т.к.
т.к. 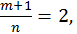 то имеем второй случай интегрируемости. Заметив, что знаменатель
то имеем второй случай интегрируемости. Заметив, что знаменатель 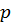 равен
равен 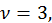 положим
положим
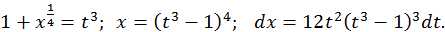

Интеграл вида 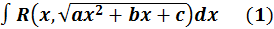
(подстановки Эйлера)
Такой интеграл приводится к интегралу от рациональной функции нового переменного с помощью следующих подстановок Эйлера.
1. Первая подстановка Эйлера.
Если 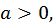 то
то 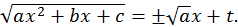
Перед 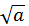 для определенности возьмем знак +.
для определенности возьмем знак +.

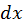 также будет выражаться рационально через
также будет выражаться рационально через 
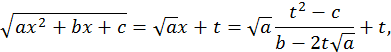
т.е. 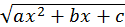 оказывается рациональной функцией от
оказывается рациональной функцией от 
Так как  и
и 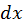 выражаются рационально через
выражаются рационально через  то, следовательно, данный интеграл
то, следовательно, данный интеграл  преобразуется в интеграл от рациональной функции от
преобразуется в интеграл от рациональной функции от 
Пример. 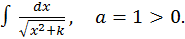 Полагаем
Полагаем 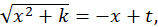
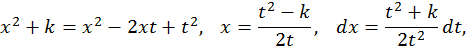
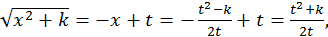
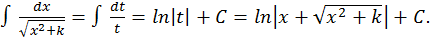
2. Вторая подстановка Эйлера.
Если 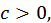 то
то 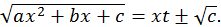
Перед 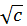 для определенности возьмем знак +.
для определенности возьмем знак +.

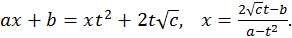
Так как 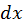 и
и 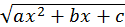 тоже выражаются рационально через
тоже выражаются рационально через  то, подставляя значения
то, подставляя значения 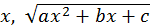 и
и 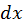 в
в  сведем этот интеграл к интегралу от рациональной функции от
сведем этот интеграл к интегралу от рациональной функции от 
3. Третья подстановка Эйлера.
Пусть 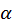 и
и 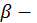 действительные корни трехчлена
действительные корни трехчлена 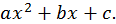
Полагаем 
Так как 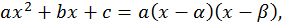 то
то
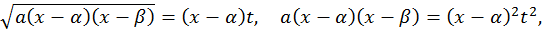
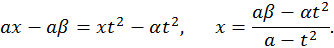
Так как 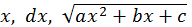 рационально зависят от
рационально зависят от  то данный интеграл преобразуется в интеграл от рациональной функции от
то данный интеграл преобразуется в интеграл от рациональной функции от 
Эта подстановка Эйлера применима как для 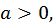 так и для
так и для 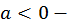 лишь бы многочлен
лишь бы многочлен 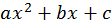 имел два действительных корня.
имел два действительных корня.
Лекция 14.
Поиск по сайту: