 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Полный дифференциал функции двух переменных
По определению полного приращения функции 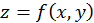 имеем:
имеем:

Предположим, что 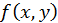 в рассматриваемой точке
в рассматриваемой точке  имеет непрерывные частные производные. Выразим
имеет непрерывные частные производные. Выразим 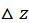 через частные производные. Для этого в правой части равенства
через частные производные. Для этого в правой части равенства  прибавим и вычтем
прибавим и вычтем 

Выражение, стоящее в первой квадратной скобке равенства 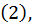 можно рассматривать как разность двух значений функции одного переменного
можно рассматривать как разность двух значений функции одного переменного  (второй аргумент сохраняет одно и то же значение
(второй аргумент сохраняет одно и то же значение  ). Применяя к этой разности теорему Лагранжа, получим:
). Применяя к этой разности теорему Лагранжа, получим:

где  заключено между
заключено между  и
и 
Выражение, стоящее во второй квадратной скобке равенства 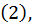 можно рассматривать как разность двух значений функции одного переменного
можно рассматривать как разность двух значений функции одного переменного  (значение
(значение  остается постоянным). Применяя к этой разности теорему Лагранжа, получим:
остается постоянным). Применяя к этой разности теорему Лагранжа, получим:

где  заключено между
заключено между  и
и 
Внося выражения 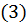 и
и 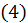 в равенство
в равенство 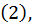 получим:
получим:

Так как, по предположению, частные производные непрерывны, то

(так как  и
и  заключены, соответственно, между
заключены, соответственно, между  и
и 
 и
и 
то при  и
и 
 и
и  стремятся, соответственно, к
стремятся, соответственно, к  и
и 
Равенства 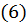 можно переписать в виде:
можно переписать в виде:

где величины  и
и  стремятся к нулю, когда
стремятся к нулю, когда  и
и 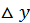 стремятся к нулю (т.е. когда
стремятся к нулю (т.е. когда  ).
).
В силу равенств  соотношение
соотношение  принимает вид:
принимает вид:
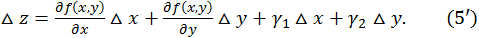
Сумма двух последних слагаемых правой части является бесконечно малой высшего порядка относительно  Действительно, отношение
Действительно, отношение 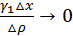 при
при 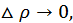 т.к.
т.к.  является бесконечно малой величиной, а
является бесконечно малой величиной, а  ограниченной
ограниченной  Аналогично проверяется, что
Аналогично проверяется, что  при
при 
Сумма первых двух слагаемых есть выражение линейное относительно  и
и  При
При  и
и  это выражение представляет собой главную часть приращения, отличаясь от
это выражение представляет собой главную часть приращения, отличаясь от 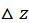 на бесконечно малую высшего порядка относительно
на бесконечно малую высшего порядка относительно 
Функция  полное приращение
полное приращение 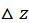 которой в данной точке
которой в данной точке  может быть представлено в виде суммы двух слагаемых: выражения, линейного относительно
может быть представлено в виде суммы двух слагаемых: выражения, линейного относительно  и
и  и величины бесконечно малой высшего порядка относительно
и величины бесконечно малой высшего порядка относительно 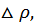 называется дифференцируемой в данной точке, а линейная часть приращения называется полным дифференциалом и обозначается через
называется дифференцируемой в данной точке, а линейная часть приращения называется полным дифференциалом и обозначается через  или
или 
Из равенства  следует, что если функция
следует, что если функция 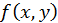 имеет непрерывные частные производные в данной точке, то она дифференцируема в этой точке и имеет полный дифференциал
имеет непрерывные частные производные в данной точке, то она дифференцируема в этой точке и имеет полный дифференциал

Равенство  можно переписать в виде:
можно переписать в виде:

и с точностью до бесконечно малых высшего порядка относительно 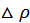 можно написать следующее приближенное равенство:
можно написать следующее приближенное равенство: 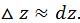
Приращения независимых переменных  и
и 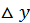 мы будем называть дифференциалами независимых переменных
мы будем называть дифференциалами независимых переменных  и
и  и обозначать, соответственно, через
и обозначать, соответственно, через 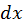 и
и  Тогда выражение полного дифференциала примет вид:
Тогда выражение полного дифференциала примет вид:

 Таким образом, если функция
Таким образом, если функция 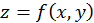 имеет непрерывные частные производные, то она дифференцируема в точке
имеет непрерывные частные производные, то она дифференцируема в точке  и ее полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.
и ее полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.
Пример. Найти полный дифференциал и полное приращение функции 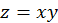 в точке
в точке  при
при 


Следовательно, 

На рисунке дана иллюстрация к этому примеру.
Предыдущие рассуждения и определения соответственным образом обобщаются на функции любого числа аргументов.
Лекция 25.
Поиск по сайту: