Метод интегрирования по частям

Пусть 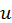и - две дифференцируемые функции от 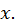Тогда, как известно, дифференциал произведения вычисляется по следующей формуле:

Отсюда, интегрируя, получаем: или

Это формула интегрирования по частям.

Выведенная формула показывает, что приводится к который может оказаться более простым, чем исходный, или даже табличным. Умение разбивать разумным образом данное подынтегральное выражение на множител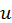и и вырабатывается в процессе решения задач. Сейчас же можно лишь сказать, что в качестве 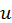обычно выбирается функция, которая упрощается дифференцированием, в качестве - оставшаяся часть подынтегрального выражения, включая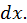

Пример.

При определении функции по дифференциалу мы можем брать любую произвольную постоянную, так как в конечный результат она не входит, что легко проверить, подставив в равенство (1) вместо выражение Поэтому удобно считать эту постоянную равной нулю.

Правило интегрирования по частям применяется во многих случаях. Так, например, интегралы вида некоторые интегралы, содержащие обратные тригонометрические функции, вычисляются с помощью интегрирования по частям.

В некоторых случаях для сведения данного интеграла к табличному формула интегрирования по частям применяется несколько раз.

Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям.

Пример.

Аналогичным образом можно вычислить следующие два интеграла.

Лекция 9.

Поиск по сайту: