Площадь криволинейной фигуры в прямоугольных координатах

Как было показано ранее, площадь криволинейной трапеции 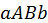вычисляется по формуле:

Здесь предполагалось, что 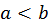и

Если же будет но то

Площадь криволинейной трапеции определяется формулой:

Площадь криволинейной фигуры вычисляется по формуле:

Эта формула получается с помощью формулы (1), т.к. указанная фигура представляет разность двух криволинейных трапеций.

Площадь фигуры определяется формулой:

В более общем случае криволинейную фигуру разбивают на части, площади которых вычисляются по приведенным формулам или определяются непосредственно.

Есл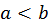и и меняет знак на отрезке то определенный интеграл равен алгебраической сумме площадей соответствующих криволинейных трапеций:

Пример. Вычислить площадь криволинейной фигуры, ограниченной параболой и прямой Данные линии пересекаются в точках и Воспользуемся формулой (3):

Рассмотрим случай, когда линия, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениями:

где

Уравнения (5) определяют некоторую функцию на отрезке Площадь криволинейной трапеции вычисляется по формуле:

Перейдем к новой переменной по формуле тогда

На основании уравнений (5) получаем:

Следовательно:

Пример. Вычислить площадь области, ограниченной эллипсом:

В силу симметрии эллипса относительно координатных осей достаточно вычисπлить площадь области, лежащей в первой четверти, и результат умножить на 4. Находим новые пределы:

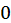
t

В частном случае, когда получим площадь круга радиуса

Поиск по сайту: