Дифференциалы высших порядков

Пусть - независимая переменная и есть дифференцируемая функция.

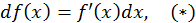
Таким образом, 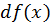- функция от и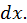

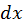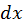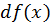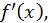В дальнейшем будем предполагать, что имеет произвольное, но фиксированное значение, независящее от независимой переменной и одно и то же для всех рассматриваемых функций. Если фиксировано, то есть некоторая функция от пропорциональная с коэффициентом пропорциональности, равным 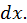Может случиться, что эта функция также имеет дифференциал (для этого достаточно, чтобы существовала 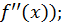в таком случае последний называется дифференциалом второго порядка (или вторым дифференциалом) функции 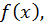а дифференциал, определяемый формулой 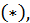носит более точное название дифференциала первого порядка (или первого дифференциала). Итак, дифференциалом второго порядка 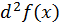функции называется дифференциал от дифференциала первого порядка этой функции, т.е. 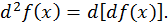Аналогично вводится дифференциал третьего порядка Так последовательно определяются дифференциалы высших порядков.

Выведем теперь формулу для дифференциала второго порядка.

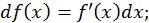
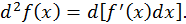
Если - независимая переменная, то 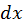не зависит от т.е. 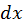по отношению к переменной играет роль постоянной. Поэтому

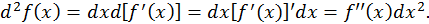
Итак,

Полагая 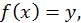можно написать или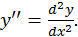

Если - независимая переменная, то по аналогии

и т.д.

Если - зависимая переменная, то 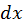не является постоянной по отношению к поэтому

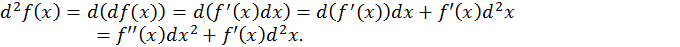
Неопределенный интеграл

Лекция 7.

Поиск по сайту: