 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос: Производная сложной функции. Производные и дифференциалы высших порядков. Теорема Ролля, Лагранжа, Коши
Теорема.
Если функция U (x) – дифференцируема в точке Хо, а функция y = f (U) – дифференцируема в соответствующей точке U = U (Xo), то сложная функция y (f (U (x))) дифференцируема в точке Хо и f ' (U (x)) в точке Х = Хо = f ' (Uo) ∙ U' (Xo). Таким образом, производная сложной функции равна произведению производных всех ее звеньев.
Для функции, зависящей от одной переменной 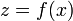 второй и третий дифференциалы выглядят так:
второй и третий дифференциалы выглядят так:


Отсюда можно вывести общий вид дифференциала n -го порядка от функции 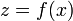 :
:

При вычислении дифференциалов высших порядков очень важно, что  есть произвольное и не зависящее от
есть произвольное и не зависящее от  , которое при дифференцировании по
, которое при дифференцировании по  следует рассматривать как постоянный множитель.
следует рассматривать как постоянный множитель.
Теорема Ролля.
Пусть f (x) непрерывна на [ a; b], f (х) дифференцируема на (а;b).
f (a) = f (b), следовательно существует по крайней мере одна точка ζ принадлежащая (а;b), в которой производная (f ' (ζ)) = 0.
Геометрический смысл:
Если значения функции на концах отрезка равны и выполняется условие теоремы Ролля, то найдется точка, в которой касательная параллельна ОХ.
Теорема Лагранжа.
Если:
f (x) непрерывна на [ а;b] и f (x) дифференцируема на (а; b), то найдется по крайней мере одна точка ζ, принадлежащая (а;b), такая что f ' (ζ) =(f (b) – f (a))/ (b – a)
Геометрический смысл:
Найдется хотя бы одна точка, в которой касательная к кривой параллельна секущей.
Эта теорема более общая по отношению к теореме Ролля.
Теорема Коши. (еще более общая).
Если: f(x) непрерывна на [а;b]
g (x) непрерывна на [а;b]
f (x) дифференцируема на (а;b)
g(x) дифференцируема на (а;b)
g ' (x) ≠ 0, то существует по крайней мере одна точка ζ, такая что:
f(b) – f(a) / g(b) – g(a) = f ' (ζ) / g ' (ζ) — формула Коши.
Замечание.
Теорема Лагранжа является следствием теоремы Коши. Если g (x) = x, тогда g '(x) = 1, следовательно: f(b) – f(a) / b – a = f ' (ζ) / 1
11 Вопрос: Правило Лопиталя:
Теорема
Пусть f(x) и g(x) имеют производную f’(x) и g'(x) (не равных нулю) в некоторой окресности точки х0,кроме быть может самой точки х0 и существ. limf(x) при x-> x0 и limg(x) при x->x0
Теорема Лопиталя:
-
 либо
либо  ;
; -
 и
и  дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности 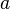 ;
; -
 в проколотой окрестности
в проколотой окрестности 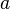 ;
; - существует
 ,
,
тогда существует  .
.
12 Вопрос: Условия возрастания и убывания функции:
Поиск по сайту: