АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теоремы о переходе к пределу в неравенствах

Читайте также:
  1. В связи с угрозой войны был создан указ о переходе
  2. Вектор электрического смещения ( электрической индукции) D. Обобщение теоремы Гаусса для вещества.
  3. ВКЛЮЧЕНИЕ ДАУ АРС ПРИ ПЕРЕХОДЕ НА РЕЗЕРВНОЕ УПРАВЛЕНИЕ.
  4. Гуманизация условий труда на предприятиях при переходе к рынку
  5. Действие винта при переходе с заднего на передний ход
  6. Действие винта при переходе с переднего хода на задний
  7. Доказательство (теоремы).
  8. Используя теоремы сложения и умножения, а также формулы комбинаторики
  9. Л.С.Выготский выделял 5 этапов в переходе к формированию понятий.
  10. Общие теоремы строительной механики
  11. Определения и теоремы
  12. Оптимизация налогов при переходе на упрощенную систему налогообложения

Теорема о переходе к пределу в равенстве

Если на и существует 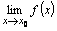, то существует и .

ПРИМЕР. Поскольку для и , то .

ТЕОРЕМА (о переходе к пределу в неравенстве)

Если или на и существуют 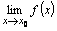– к.ч. и – к.ч., то .

Доказательство можно провести методом от противного.
Рекомендуем провести самостоятельно.

ТЕОРЕМА (о перенесении неравенства между пределами на функции)

Если существуют пределы и и выполняется неравенство , то существует окрестность ,
на которой .

Доказательство. Имеем

,

в частности, при : , т.е. . Аналогично

,

в частности, при , т.е. или .

Поскольку при , то на пересечении окрестностей имеем , т.е. указали окрестность , на которой характер неравенства между пределами переносится на функции.

Следствие. Если – конечное число и , то можно указать окрестность , на которой .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)