АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема о пределе промежуточной функции

Читайте также:
  1. A) эффективное распределение ресурсов
  2. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  3. Access. Базы данных. Определение ключей и составление запросов.
  4. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  5. I. Открытые способы определения поставщика.
  6. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  7. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  8. II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  9. III. Используемые определения и обозначения
  10. III. Определение оптимального уровня денежных средств.
  11. III. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
  12. III. Распределение часов по темам и видам обучения

ТЕОРЕМА (о пределе промежуточной функции)

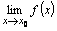Если на и существуют и и их значения конечны и равны, то существует предел промежуточной функции и его значение совпадает со значением пределов оценивающих слева и справа функций.

Доказательство рекомендуем построить самостоятельно,
используя определение предела по Коши для функций и при .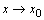

ТЕОРЕМА (об арифметике функций, имеющих конечный предел в одной и той же точке)

Пусть функции и при 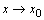имеют конечные пределы, т.е. , , 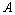и – конечные числа.

Тогда при 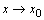имеет конечный предел каждая из функций:

1) ; 2) ; 3) (при ).

Доказательство. 1. Операция сложения функций определяется поточечно. Утверждение верно для произвольного конечного
множества функции. Здесь рассматривается сумма двух функций.

Имеем , т.е. для всякого (в частности, для ) существует так, что .

Аналогично () (, ).

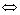Рассмотрим и оценим: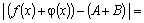

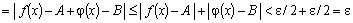
на .

Итак, , т.е. по определению предела – конечное
число, причем предел СУММЫ функций равен СУММЕ пределов слагаемых функций, если предел каждой слагаемой функции – конечное число.

Заметим, что обратное утверждение неверно, т.е. существование конечного предела суммы функций не определяет существование предела каждого слагаемого.

4 Вопрос: Первый и второй замечательные пределы. Предел функции на бесконечности. Горизонтальные и наклонные асимптоты графика функции.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)