 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
III. Используемые определения и обозначения
Построение булевых функций максимальной нелинейности
Курсовая работа студента 222 группы
Исаева Глеба Андреевича
Научный руководитель
Доцент /Агафонова И.В./
Оценка …….
Санкт-Петербург
I. Оглавление
Введение……………………………...…………………..……...…………….3
Используемые определения и обозначения..…………..……...…………….4
Конструкция бент-функции…………………………………………………..7
Заключение…………………………………………………………………...11
Список использованных источников…..…………………………………...12
II. Введение
Работа посвящена построению булевых функций максимальной нелинейности, которые нужны для достижения криптографических целей.
В 3-ей главе на множестве двоичных векторов длины n будут введены определения полинома Жегалкина, нелинейности функции и т.д.
Во 4-ой главе будут введены определения преобразования Уолша-Адамара и бент-функции, а также изучена и разобрана теорема Мэйорана-МакФарланда, которая является одним из методов получения бент-функций.
III. Используемые определения и обозначения
Для начала введем определение булевой функции. Булева функция – это такая функция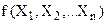 
, у которой все независимые аргументы 
и значения функции являются логическими переменными, то есть принимают только два значения: 0 и 1. Аргументы функции называются булевыми векторами.
Булеву функцию можно представить в виде таблицы истинности.
Пример 1:
| X1 | X2 | X3 | f (X1, X2, X3) |
Функция от n переменных имеет 2n значений. Так как на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n -арных булевых функций равно 22n.
Определение. Полином Жегалкина – это такая булева функция, которая допускает только 2 операции: конъюнкция и сложение по модулю 2. Также он имеет альтернативное название – алгебраическая нормальная форма (АНФ). Любую булеву функцию можно единственным образом представить в виде полинома Жегалкина.
Этот полином обычно записывают в следующем виде:
Р(X1,X2,…,Xn) = А0 + A1X1 + A2X2 + … + AnXn + A12X1X2 + A13X1X3 + +… + A1…nX1…Xn, где Аi1…inÎ{0,1}.
По приведенной таблице истинности можно построить АНФ функции. Воспользуемся алгоритмом нахождения коэффициентов полинома Жегалкина. Алгоритм таков:
1. Берем вектор значений функции и делим его пополам.
2. Первую половину переписываем в новый столбец в таком же порядке.
3. Вторую половину складываем с первой по модулю 2 и записываем результат во вторую половину нового столбца.
4. Каждые половинки делим еще на две половины.
5. Повторяем шаги 2-4 до тех пор, пока каждый кусочек не будет состоять из одного элемента.
6. Записываем полученный вектор в таблицу истинности. Этот вектор представляет собой все коэффициенты перед каждым мономом
Алгоритм описан в [2, глава 2, §2.1].
Реализуем этот алгоритм на примере 1.
Самый последний столбец и есть вектор коэффициентов АНФ функции. Теперь запишем функцию в виде полинома Жегалкина. Каждый коэффициент должен стоять напротив своего набора переменных. Для начала запишем вектор в таблицу.
| X1 | X2 | X3 | A1…n |
Таким образом, полином Жегалкина примера 1 будет иметь вид:
f(X1,X2,X3) = X2 + X1X3
Введем еще несколько определений.
Алгебраическая степень функции – это степень АНФ этой функции. Степень АНФ функции – это максимальная степень среди всех мономов xN=ÕiÎNxi, то есть наибольшая мощность подмножества N. Если степень функции будет равна 1, то такая булева функция называется аффинной. Ее АНФ имеет вид:
f(X1,…,Xn) = A1X1 + A2X2 + … + AnXn + B = <A,X> + B, где ВÎ{0,1}.
Вес Хэмминга булевой функции – это число единиц вектора значений этой функции. Обозначим вес в виде wt(f).
Расстоянием Хэмминга между двумя функциями f и g называется вес функции f + g или, иначе говоря, число таких векторов x, при которых f(x)≠g(x).
Нелинейность N(f) булевой функции f – это расстояние Хэмминга между f и множеством аффинных функций Ln. Для того, чтобы посчитать нелинейность, рекомендуется сделать преобразование Уолша-Адамара 2-го рода и воспользоваться специальной формулой (см. ниже).
Поиск по сайту: