 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос: Действия с матрицами. Определители второго и третьего порядка
Определение. Матрицей размера  называется прямоугольная таблица из чисел
называется прямоугольная таблица из чисел  , где
, где  ,
,  ,
,
 ,
,
состоящая из 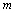 строк и
строк и  столбцов.
столбцов.
Определение. Суммой  матриц
матриц 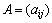 и
и  размера
размера  называется матрица
называется матрица 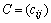 того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В:
того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В: 
 ,
,  ,
,  .
.
Определение. Произведением αА матрицы 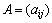 на число α называется матрица
на число α называется матрица  , элементы которой
, элементы которой 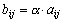 .
.
Пример 7. Вычислить 3А+2В, если
 ,
,  .
.
Решение. Вычислим  ,
,  . Тогда
. Тогда  .
.
Определение. Произведением АВ матрицы 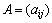 размера
размера  на матрицу
на матрицу  размера
размера  называется матрица
называется матрица  размера
размера  , элемент которой
, элемент которой  , стоящий в i-ой строке и j-ом столбце, равен сумме произведений соответствующих элементов i-ой строки матрицы А и j-ого столбца матрицы В:
, стоящий в i-ой строке и j-ом столбце, равен сумме произведений соответствующих элементов i-ой строки матрицы А и j-ого столбца матрицы В:
 ,
,

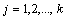 .
.
Так как строки и столбцы матриц участвуют в произведении АВ неравноправно, то АВ≠ВА.
Пример 8. Вычислить  .
.
Решение. Умножим элементы первой строки первой матрицы на соответствующие элементы первого столбца второй матрицы и сложим все произведения. Полученный элемент поставим в первую строку и первый столбец матрицы-произведения. Далее вычислим остальные элементы произведения матриц.
 .
.
Матрицу  называют единичной. Легко проверить, что
называют единичной. Легко проверить, что 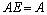 , если, конечно, число столбцов матрицы А равно числу строк матрицы Е, и ЕА=А.
, если, конечно, число столбцов матрицы А равно числу строк матрицы Е, и ЕА=А.
Если матрица А имеет одинаковое число строк и столбцов, то ее называют квадратной.
Определение. Определителем квадратной матрицы А называется определитель, составленный из ее элементов.
Обозначают определитель матрицы А либо det A (от слова детерминант, т.е. определитель), либо | A |, либо D.
Определение. Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля. В противном случае матрицу называют вырожденной.
Определение. Матрица  такая, что
такая, что  , называется обратной матрице А.
, называется обратной матрице А.
Если А – невырожденная матрица, то существует и при этом единственная матрица, обратная к матрице А. При этом  , где
, где  - алгебраические дополнения к элементам исходной матрицы.
- алгебраические дополнения к элементам исходной матрицы.
Замечание. Следует обратить внимание на то, что алгебраические дополнения к элементам строк матрицы А располагают в столбцах с теми же номерами, что и строки данной матрицы А.
Пример 9. Найти матрицу, обратную к матрице  .
.
Решение. Вычислим 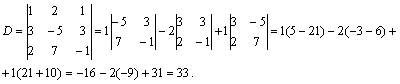
Найдем алгебраические дополнения соответствующих элементов матрицы А:
 ,
,  ,
,
 ,
,
 ,
,  ,
,
 ,
,
 ,
,  ,
,
 .
.
Имеем  .
.
22.2 Определители 2 и 3 порядка.
Определителем называется число, записанное в виде квадратной таблицы:
 .
.
Таблица ограничивается слева и справа вертикальными линиями,  -называется элементами определителя (
-называется элементами определителя (  -номер строки,
-номер строки, 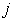 -номер столбца).
-номер столбца).
Главная диагональ определителя содержит элементы  , противоположная диагональ называется побочной.
, противоположная диагональ называется побочной.
Порядком определителя называется число строк (столбцов) квадратной таблицы.
Определитель II порядка вычисляется по формуле:


Определитель III порядка можно вычислить по правилу Сарруса:

Основные свойства определителей:
1.1. Значение определителя не изменится, если:
- строки заменить на столбцы, такое действие называется транспонирование, т.е. действия, выполняемые со строками, справедливы и для столбцов;
- все элементы одной строки умножить на какое-либо число и прибавить к соответствующим элементам другой строки.
Такие действия с элементами определителя называются элементарными преобразованиями.
1.2. Определитель меняет знак на противоположный, если две каких-либо строки поменять местами.
1.3. Определитель равен нулю, если:
- все элементы какой-либо строки равны нулю;
- соответствующие элементы каких-либо двух строк равны;
- соответствующие элементы каких-либо двух строк пропорциональны.
2. Алгебраическое дополнение и минор.
Элементарные преобразования.
Вычисление определителей n-го порядка (n >4)
Минором  к элементу
к элементу  называется определитель, полученный из исходного, вычеркиванием
называется определитель, полученный из исходного, вычеркиванием  -й строки и
-й строки и  -го столбца.
-го столбца.
Таким образом, порядок минора меньше порядка исходного определителя на единицу.
Алгебраическое дополнение  – минор
– минор  с соответствующим знаком, т.е.
с соответствующим знаком, т.е.
 .
.
Вычисление определителей n-го порядка выполняется по формуле:

т.е. определитель представляется в виде разложения по элементам  -й строки.
-й строки.
Пример
Вычислить определитель IV порядка:

Поиск по сайту: