Вопрос: Бесконечно малые функции и их свойства. Эквивалентные бесконечно малые. Бесконечно большие функции. Вертикальные асимптоты графика функции

2.1. Бесконечно малые и их свойства.

Функция α(х) называется бесконечно малой при 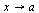, если ,

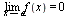т. е. для любого числа ε > 0 существует такое число δ > 0, что для всех х, удовлетворяющих неравенству

,

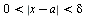выполняется неравенство

.

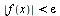Бесконечно малую функцию α(х) называют бесконечно малой величиной или просто бесконечно малой.

Функция f (х) называется ограниченной при 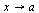, если существуют положительные числа М и δ, такие, что при условии
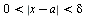, выполняется неравенство
.

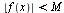Например, любая бесконечно малая α(х) является ограниченной функцией при .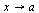

В дальнейшем будем рассматривать бесконечно малые при .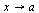

Свойства бесконечно малых.

1. Если функции 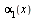и являются бесконечно малыми, то функция 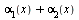также есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.

2. Произведение ограниченной при 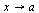функции на бесконечно малую есть функция бесконечно малая.

3. Произведение постоянной на бесконечно малую есть бесконечно малая.

4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.

Поиск по сайту: