Доказательство (теоремы)

I. Рассмотрим ситуацию, когда функция принимает не более чем счётное число значений.

Пусть функции .

,

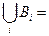
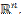
Введём в рассмотрение события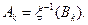

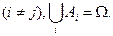
Рассмотрим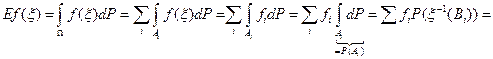

.

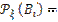
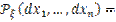
II. Рассмотрим ситуацию, когда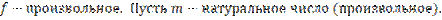

Определим функцию равенством 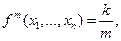если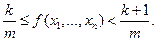

Тогда, так определяемая функция принимает не более чем счетное число значений.

Имеем

из определения .

.

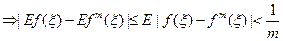
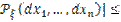
Рассмотрим +

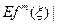
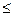+ - {где - 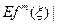=0 по первому пункту }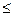

+| .

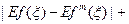
Теорема доказана.

Ещё одно следствие, которое мы сформулируем как отдельный результат:

Теорема.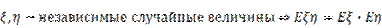

Доказательство. Пусть , тогда .

.

Замечание. В обратную сторону утверждение неверно.

Предлагается самостоятельно привести пример, когда обратное утверждение неверно.

Лекция 9 (2.11.10)

Поиск по сайту: