Формула умножения вероятностей

Пусть - случайные события. . Тогда верно равенство

.

Рассмотрим функцию такую, что для случайного события 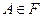где .

Теорема. Функция -вероятность.

Доказательство. Проверим 3 условия вероятности.

1) Возьмём произвольное событие .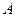

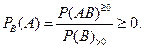
2)

3) Рассмотрим набор попарно несовместных событий (набор может быть и бесконечный)

, .

из 1),2),3) 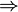-вероятность.

Следствие. Все свойства вероятности выполнены и для условной вероятности (8 свойств).

Т.е. свойства вероятности верны и для условной вероятности. В частности,

Формула полной вероятности. Формула Байеса.

Поиск по сайту: