Определение. -набор случайных событий

-набор случайных событий. Мы будем называть его полной системойсобытий ó

1) ;

2) ;

Теорема (Формула полной вероятности).

Пусть - полная система событий. .

Тогда для случайного события вероятность этого события можно вычислить по формуле

.

Доказательство.

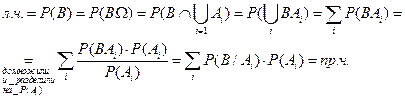
Замечание. Формула полной вероятности верна, если вместо полной системы событий будем считать, что .

Теорема( Формула Байеса).

Пусть - полная система событий. , , .

Тогда .

Доказательство.

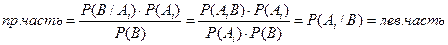
Пример.

Представим, что хотим провести эксперимент. Имеется ящик, а в нем 10 белых и 6 чёрных шариков. Два шарика по дороге потерялись, неизвестно какие. Затем из ящика наугад достали 3 шарика.

1) Р(2 белых и 1 чёрный)=?

Введём 3 следующих события:

С₁=потеряли 2 белых шарика;

С₂=потеряли 1 чёрный и 1 белый шарик;

С₃=потеряли 2 чёрных шарика.

С₁, С₂, С₃-полная система событий.

Пусть событие 2 белых и 1 чёрный,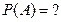

Воспользуемся формулой полной вероятности

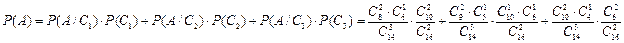
2)Рассмотрим теперь другой случай

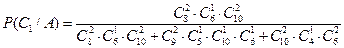
Пример (парадокс Монти Холла): Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трех дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой (он знает) находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?

Поиск по сайту: