 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема (Критерий возвратности)
1) 
- возвратное состояние 
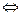
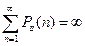(ряд расходится);
2) - невозвратное состояние 
.
Доказательство теоремы.
Пусть имеется последовательность чисел 
(
), 
.
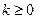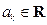, если такой ряд суммируемый.
- производящая функция последовательности .
Рассмотрим 
и 
, тогда их производящие функции:
; 
;
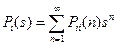Имеем по формуле полной вероятности:
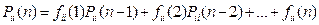; тогда
. Отсюда следует равенство
(равенство после суммирования) (*).
определена на 
, т.к. при 
ряд может расходиться.
определена на 
, т.к. ряд всегда конечен.
Заметим, что 
.
Из (*) следует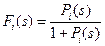 
; и далее (
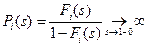если - возвратное состояние), т.е. ряд расходится.
Если ряд расходится, то при 
- возвратное состояние.
Лекция 15 (14.12.10)
Пусть 
цепь Маркова. Разобьем все состояния цепи Маркова на следующие классы:
класс несущественных состояний. Пусть существует существенное состояние 
Тогда
существенные состояния, сообщающиеся с . Пусть существует существенное состояние 
, которое не входит в класс S1. Тогда
существенные состояния, сообщающиеся с .
…
Понятно, что эти классы не пересекаются, т.е.
Перенумеруем состояния. Сначала занумеруем состояния из класса S0, затем из класса S1 и т.д.
Тогда матрица переходных вероятностей за n шагов будет иметь следующий вид:
| 
| 
| … | |
| 
| 
|
| |
|
|  0
| |||
|
|  0
| |||
|
Каждый блок в отдельности – стохастическая матрица.
Определение. Цепь Маркова называется неразложимой, если она состоит из одного класса сообщающихся между собой состояний.
Теорема. (О солидарности для возвратности)
Пусть ЦМ неразложимая или все состояния возвратные, или все невозвратные.
Доказательство.
Пусть 
возвратное состояние и пусть состояние 
.
Пусть 
Напомним, что по критерию возвратности
возвратное состояние 
Рассмотрим 
состояние 
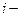тоже возвратно.
Случайные блуждания по целым точкам в 
н. о. р. с. в. 
,
цепь Маркова - случайное блуждание по целым точкам на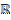 
. (
).
Проверим, будут ли состояния этой ЦМ возвратными. Понятно, что достаточно провести проверку только для одного состояния, т.к. все состояния сообщаются между собой.
Очевидно, что
Рассмотрим 
= 
Используем формулу Стирлинга (
где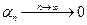 
) и получаем
где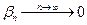 
. Тогда
(заметим, что в этом случае 
)
состояние 0 – возвратное, а если 
состояние 0 – невозвратное.
Итак, если случайное блуждание по целым точкам на вещественной прямой симметрично (т.е. p=q), то оно возвратное и наоборот.
Случайное блуждание по решётке «целочисленных» точек в 
Симметричные случайные блуждания на плоскости тоже будут возвратными.
Рассмотрим событие, которое означает возврат в начальное состояние через 
шагов.
Каждая из таких ситуаций может быть записана цепочкой длины последовательности шагов: (П П В Н … Л … В) -
Здесь П означает шаг вправо, Л – шаг влево, В – шаг вверх и Н – шаг вниз, причем для возврата в начальное состояние число шагов в каждом направлении должно быть следующим:
в сумме шагов
Тогда
Ряд с такими членами расходится, и следовательно, такое случайное блуждание тоже возвратное.
Случайное блуждание в 
Рассмотрим симметричные случайные блуждания по точкам с целочисленными координатами в трехмерном пространстве. Здесь шаг вверх – ВВ, шаг вниз – ВН, шаг вправо – П, шаг влево – Л, шаг вперед – ВП и шаг назад – Н и пусть
Для возврата в начальное состояние число шагов в каждом направлении должно быть
следующим:
в сумме шагов
Тогда
=
Заметим, что 
Поскольку
то начальное состояние невозвратное, а следовательно и все состояния невозвратные.
Поиск по сайту: