Определение 2. - независимые случайные величины

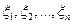- независимые случайные величины

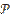
или, что то же самое

.

Совсем нетрудно заметить, что определения 1 и 2 равносильны.

Пусть на некотором вероятностном пространстве определена случайная величина

(, измеримая, т.е. ).

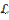
Рассмотрим множество случайных событий 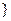- множество всех прообразов измеримых подмножеств прямой; очевидно, что .

Заметим, что выполняются следующие соотношения:

1.

2. \

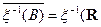3. - измеримые подмножества прямой, тогда , где .

Из соотношений 1-3 следует, что - - 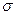алгебра.

Определение.

- это 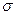- алгебра, порожденная случайной величиной .

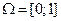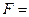
Примеры: , , 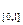- мера Лебега.

1) ;

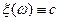
2) (где ) .

3) .

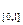Поиск по сайту: