Лемма (Бореля - Кантелли)

Пусть - последовательность случайных событий.

a) Если , то = 0;

b) Если - независимые случайные события и , то .

Следствие: Для независимых событий

сходимость ряда: ;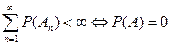

расходимость ряда: .

Доказательство (леммы).

a) Рассмотрим P(A)=

- т.к. это хвост сходящегося ряда .

b) P(A)=

{ }

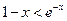
Далее напомним определение усиленного закона больших чисел (УЗБЧ):

УЗБЧ для

и сходимость к 0 в правой части - почти наверное.

Теорема. - независимые случайные величины, существуют и

Тогда для выполнен УЗБЧ.

Доказательство. Пусть (что не умаляет общности)

Покажем, что

.

И число слагаемых ≤ m n²

Возьмём последовательность такую, что

Рассмотрим событие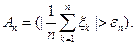

Тогда

{если взять (будет убыв. послед., как и надо) }

Что нам обеспечивает сходимость ряда, мы можем сказать, что

Рассмотрим событие бесконечное число раз где

Это означает, что п. н.

Это и есть УЗБЧ, теорема доказана.

Лекция 13 (30.11 10)

Поиск по сайту: