 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Ковариация и коэффициенты корреляции
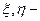 случайные величины, определенные на одном и том же вероятностном пространстве
случайные величины, определенные на одном и том же вероятностном пространстве  .
.
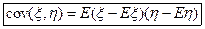
Свойства ковариации:
1. 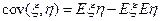 ;
;
2. 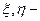 независимые сл. величины
независимые сл. величины 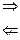
 ;
;
3. 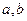 - числа
- числа 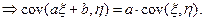
Пусть 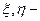 случайные величины, у которых сущ.
случайные величины, у которых сущ. 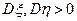 .
.
Число 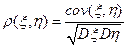 называется коэффициентом корреляции.
называется коэффициентом корреляции.
Замечание. (к определению)
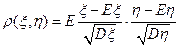 . При этом
. При этом 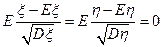 .
.
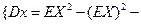 было свойство
было свойство 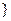 .
.
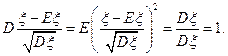
Таким образом, говорим, что провели центрирование и нормирование случайной величины.
Свойства коэффициента корреляции:
1. 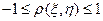 (т. е.
(т. е.  )
)
2. 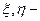 независимые сл. величины
независимые сл. величины 
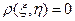
3. Если 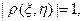 то
то 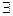
 (т. е.
(т. е.  и
и  линейно связные с вер.=1)
линейно связные с вер.=1)
и 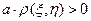 (положительное число)
(положительное число)
(т. е. у  тот же знак, что и у коэффициента корреляции)
тот же знак, что и у коэффициента корреляции)
Доказательство свойств.
1) 
Таким образом 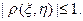
2) Следует из свойств для ковариации.
3) Пусть 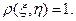
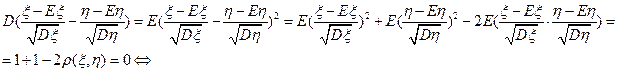
(заметим, что если 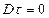 , то
, то 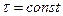 )
)

Пусть 

(если 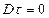 , то
, то 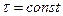 )
)
Задача. 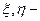 зависимые сл. величины: (
зависимые сл. величины: ( ) – случайный вектор – равномерно распределён в
) – случайный вектор – равномерно распределён в
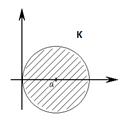 круге К: т.е. имеется плотность
круге К: т.е. имеется плотность
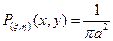

 , где
, где 
 =
= 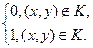
Чему равен 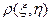 -?
-?
Лекция 11 (16.11.10)
Поиск по сайту: