Случайные величины с дискретным законом распределения

Определение:

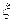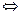
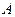
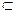
- с дискретным законом распределения 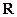: 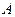-не более чем счетное (нбчс) и .

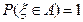Так как 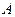- нбчс, то занумеруем элементы множества =

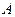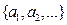
Составим таблицу:

			…
			…

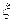
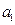
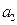
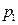
где = .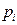

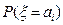Эту таблицу будем называть законом распределения случайной величины .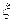

Пример: Пусть 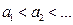(т.е. все значения упорядочены по возрастанию, хотя это и не обязательно). Рассмотрим функцию распределения.

и =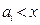

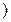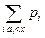
График функции распределения – ступенчатая функция.

Свойства :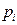

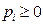и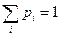

Это следует из равенств:

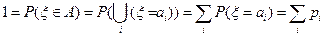
Примеры (наиболее распространенных случайных величин с дискретным законом распределения)

1)

- случайная величина с вырожденным распределением в точке .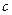

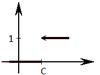Ее закон

распределения и

график функции

распределения:

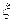
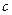
2) 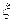- с распределением Бернулли

Таблица: ()

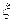
3)

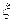- с биномиальным распределением с параметрами и

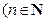
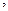
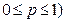
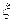принимает значения: 0, 1, 2, …, и 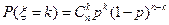число успехов в испытаниях Бернулли

4)

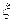- с распределением Пуассона с параметром

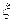принимает значения: 0, 1, 2, 3, … и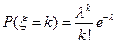

Лекция 6 (12.10.10)

Поиск по сайту: