Теорема

. Если то периодическое состояние и период состояния j. Если то непериодическое состояние.

Заметим, что

аддитивный класс

Последнее следует из следующих соотношений:

Лемма. Пусть аддитивный класс и период. Тогда :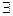

Доказательство. 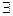и .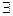

(Пусть - множество натуральных чисел. Заметим: если ) Итак,

Где

Таким образом

Рассмотрим

Получаем, что , (*)

Пусть и . Представим в виде (разделили на с остатком), где . Имеем далее:

, т.е. и . Следовательно, выполняется (*), откуда и следует утверждение леммы.

Теорема. Пусть существенные сообщающиеся состояния неразложимой ЦМ. Тогда

Доказательство. В силу неразложимости ЦМ состояния i и j сообщаются, т.е. найдутся натуральные

т.е.

Пусть , т. е.

Рассмотрим

Аналогично, Теорема доказана.

Пусть - произвольное состояние ЦМ с периодом .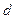

Разобьем все множество состояний на 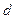классов: .

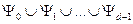Состояние существует .

Покажем, что .

и пусть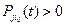

для некоторого t. Тогда

, (1)

(2)

Из (1) и (2) следует, что , т.е. и никак иначе.

Утверждение. Докажем, что если , то ; (это означает, что с вероятностью равной 1 переходы из состояний одного класса в состояния другого класса возможны только по следующей схеме:

)

Доказательство. . Докажем это.

Предположим противное. Пусть существует и пусть , т.е.

Тогда

(по определению разбиения множества всех состояний).

называются циклическими подклассами.

Матрица переходных вероятностей будет выглядеть следующим образом (заштрихованные блоки являются стохастическими матрицами).

				...
		0
...

Пусть далее - ЦМ с конечным числом состояний (конечная ЦМ {КЦМ}).

Утверждение. В конечной ЦМ все существенные состояния являются возвратными и все возвратные состояния существенны, т.е. в КЦМ понятия существенности и возвратности равносильны.

Доказательство.

I. Докажем сначала, что если 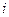- возвратное, то 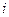- существенное.

Предположим противное: 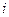- возвратное и несущественное существует такое, что и .

(т.к. возвратное). Пусть (возможность перейти из 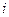в за конечное число шагов)= А и пусть событие Б= (никогда не вернуться в состояние 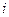). Тогда

никогда не вернуться в 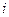и, кроме того, имеем следующее включение:

(А) (Б) Отсюда следует, что

(противоречие).

II. Теперь покажем, что

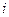- существенное 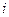- возвратное.

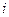- возвратное (критерий возвратности состояний).

Кроме того, имеем

Рассмотрим (для конкретного )

Заметим, что суммировать можно только по существенным состояниям (в противном случае получаются нули).

существует

, где .

Если 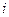- нулевое (верно для любого ).

Имеем, что (а число слагаемых конечно, т.к. КЦМ).

Противоречие с тем, что 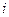- нулевое 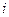- возвратное.

Лекция 17 (15.02.11)

Поиск по сайту: