Определение

Функция 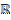, 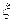-измерима 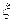- случайная величина.

Это означает, что для любого измеримого подмножества 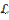( 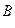-множество, измеримое по Лебегу по прямой) прообраз .

Рассмотрим случай, когда функция является случайной величиной и когда нет.

Возьмём это мера каждого отрезка, т.е.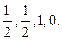

a)

не случайная величина.

б) это случайная величина.

Любая является случайной величиной.

Задание: Описать все возможные случайные величины для такого вероятностного пространства.

Что же нам даёт случайная величина?

Рассмотрим функцию , называетсяраспределением случайной величины .

Теорема. -вероятность, заданная на .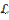

Доказательство. Проверим 3 свойства вероятности.

1)

2) = =

3)

()= .

Смысл введения случайной величины:

(. Мы перешли к другому вероятностному пространству.

Поиск по сайту: