 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Испытания Бернулли. Формула Бернулли
Рассмотримвероятностное пространство ( ).
).
Определения:
1.  - испытание – это разбиение множества элементарных событий на попарно несовместные.
- испытание – это разбиение множества элементарных событий на попарно несовместные.
Т.е.  = {
= {  },
},  и
и  ;
;
2. Рассмотрим два испытания:  1= {
1= {  };
};  2 = {
2 = {  }
}
 1 и
1 и  2 - независимые испытания, если
2 - независимые испытания, если 
 - независимые.
- независимые.
Пусть имеются несколько испытаний  1,
1,  2, …,
2, …,  k. Они независимы ó
k. Они независимы ó 
 - взаимно независимые события.
- взаимно независимые события.
Примеры: 1) Рассмотрим двукратное подбрасывание симметричной монеты:
 = { (ОО), (ОР), (РО), (РР)}; Все исходы равновероятны.
= { (ОО), (ОР), (РО), (РР)}; Все исходы равновероятны.
 1 = {
1 = {  }, где
}, где  ={(ОО),(ОР)} - первый элемент – О
={(ОО),(ОР)} - первый элемент – О
 = {(РО),(РР)} - первый элемент – Р
= {(РО),(РР)} - первый элемент – Р
 2 = {
2 = {  }, где
}, где  = {(ОО),(РО)} - второй элемент – О
= {(ОО),(РО)} - второй элемент – О
 = {(ОР),(РР)} - второй элемент – Р
= {(ОР),(РР)} - второй элемент – Р

 =
= 
 {(ОО)}
{(ОО)}  =
=  =
=  *
*  =
= 
 =
=  =
=  , где
, где  =
= 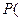 {(ОО),(ОР)}
{(ОО),(ОР)}  ,
,  =
= 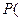 {(ОО),(РО)}
{(ОО),(РО)}  .
.
Таким образом, убедились в независимости испытаний.
2) одновременное подбрасывание монетки и кубика:  = { (0,1), (0,2), …,(0,6), (Р1), …,(Р6)}, все исходы равновероятны,
= { (0,1), (0,2), …,(0,6), (Р1), …,(Р6)}, все исходы равновероятны,  =
= 
 1 = {
1 = {  }, где
}, где  ={на монетке выпал орел},
={на монетке выпал орел},  = {на монетке выпала решка}
= {на монетке выпала решка}
 2 = {
2 = {  }, где
}, где  = {на кубике выпала i-я грань}.
= {на кубике выпала i-я грань}.
Эти испытания независимы.
Определение:
n испытаний Бернулли – это n независимых испытаний с двумя исходами в каждом испытании, условно называемые «успехом» и «неудачей», и с постоянной вероятностью «успеха» во всех испытаниях.
Пусть  1,
1,  2, …,
2, …,  n - независимые испытания
n - независимые испытания
 k = {Уk, Нk},
k = {Уk, Нk}, 
 Уk
Уk  = p
= p  k
k
Пусть событие 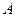 = {в n испытаниях произошло ровно k успехов}
= {в n испытаниях произошло ровно k успехов}
Обозначение:  =
= 
Рассматриваем объединение попарно несовместных событий: 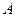 = (УУ…УН…Н)
= (УУ…УН…Н)  (УУ…УНУН…Н)
(УУ…УНУН…Н)  …,
…,
где в каждой комбинации из символов У и Н k штук У и (n-k) штук Н;
Рассмотрим  цепочку и посчитаем
цепочку и посчитаем 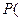 УУНУ…НУ
УУНУ…НУ  , где k успехов и (n-k) неудач.
, где k успехов и (n-k) неудач.
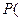 УУНУ…НУ
УУНУ…НУ  =
= 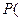 У1
У1  У2
У2  Н3
Н3 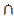 Н4
Н4 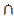 …
…  Нn-1
Нn-1 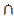 Уn
Уn  = pk * (1-p)n-k = pk * qn-k , где qn-k=(1-p)n-k
= pk * (1-p)n-k = pk * qn-k , где qn-k=(1-p)n-k
Сколько таких цепочек? Ответ -  . Итак, получаем
. Итак, получаем
 =
= 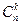 *
*  *
*  - Формула Бернулли
- Формула Бернулли
Следствия:
1)  =
= 
2)  =
= 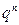
3)  хотя бы один успех
хотя бы один успех  =
= 
Задача: Рассмотрим n испытаний Бернулли,  1
1  У
У  =
=  , где 0<
, где 0<  <1
<1
Пусть 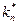 - наивероятнейшее число успехов в n испытаниях, n, p – известны,
- наивероятнейшее число успехов в n испытаниях, n, p – известны, 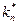 =?
=?
Найдем все такие k, для которых выполняется неравенство 









Возможны 2 ситуации:
1. 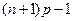



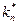 = [
= [  ] – одно наивероятнейшее число успехов.
] – одно наивероятнейшее число успехов.
2. 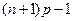







Если  , то
, то 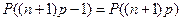
То  два наивероятнейших числа успехов.
два наивероятнейших числа успехов.
Пример: Возьмем симметричную монету.
Каково наиболее вероятное число успехов (орлов) при подбрасывании 10 раз? Ответ - 5.
Каково наиболее вероятное число успехов (орлов) при подбрасывании 13 раз? Ответ - 6 и 7.
Поиск по сайту: