Классическое определение вероятности или схема равновозможных исходов

Множество элементарных событий состоит из конечного числа элементарных событий, т.е. Ω = { ω₁ … ω_n}, F= 2 ^Ω

Все исходы равновозможны ó P({ω₁}) = P({ω₂}) = … = P({ω_n}) =

Рассмотрим произвольное событие А= { ω_i₁, ω_i₂ … ω_ik }. Тогда по 3^ей аксиоме

P(A) = k / n = Число благоприятствующих для события А исходов / Число всех возможных исходов. Это классическое определение вероятности.

Пример.

Рассмотрим ящик, в котором M белых и N черных шаров. Вытаскиваем 10 шаров.

Событие А= {вытащить 2белых и 8черных шаров}

Пронумеруем шарики: 10< M, 10< N

Результат – десятка конкретных шариков.

Общее число исходов =

Число благоприятных исходов = *

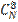
P (A) =

Задача для самостоятельного решения (о нерадивом секретаре): У секретаря есть N конвертов и N писем (и то, и другое занумеровано). Он случайным образом кладет письма в конверты. Какова вероятность того, что хотя бы в одном случае будет совпадение номера письма и номера конверта? Если мы вероятность этого события обозначим , получить .

Лекция 2. (14.09.10)

Поиск по сайту: