Теорема (Финальные или стационарные вероятности)

Пусть существует : .

Тогда: 1) существует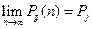

2) вектор 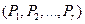является единственным решением следующей системы:

при .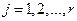

(Каков смысл:

Представим, что мы наблюдаем за перемещением частицы по состояниям системы и заснули, а частичка продолжала «гулять». Тогда вектор 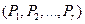- это вероятности того, что мы найдем частичку в соответствующем состоянии, когда проснемся.)

Доказательство: Введем обозначения , .

Имеем

= (ур-е Маркова-Чепмена-Колмогорова)= ;

.

Т.е. и .

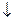А т.к. существуют .

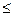
Возьмем произвольное - натуральное число,

и пусть состояния таковы, что , . Имеем

=(ур-е Маркова-Чепмена-Колмогорова)=

= = =

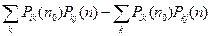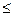
{ + , где = , = }

{ }

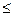
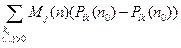
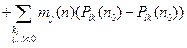
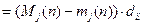
Далее,

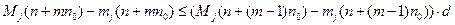
, чем и доказали первый пункт.

Докажем пункт 2.

Во-первых заметим, что

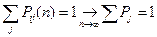
Из равенства и соотношений и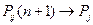

Получаем .

Осталось доказать единственность:

Пусть - какое-то решение нашей системы.

Рассмотрим =

= … = ,

Таким образом, из равенства и соотношений и = ,

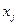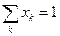следует равенство P_j =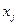

и единственность доказана.

Поиск по сайту: