Цепи Маркова

Пусть последовательность случайных величин, значения которых лежат в множестве ; н. б. ч. с. Можно считать, что .

Определение. Последовательность случайных величин будем называть цепью Маркова, если и

Множество будем называть множеством состояний.

играет роль времени, - состояние системы, за которой мы наблюдаем.

Марковское свойство:

- прошлое и будущее независимы при фиксированном настоящем.

Определим , где 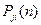- переходная вероятность из состояния в состояние 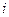в момент времени .

Если 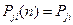(т. е. не зависит от момента времени) однородная цепь Маркова.

Чтобы знать все вероятности , необходимо знать

·

· .

Например, = .

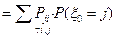Рассмотрим матрицу, которую обозначим Такую матрицу мы будем называть матрицей переходных вероятностей.

Для матрицы 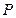выполняются условия:

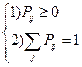
Любая матрица с такими совйствами называется стохастической.

Итак, чтобы уметь описывать цепь Маркова, необходимо знать

1) Вектор начальных состояний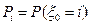

и матрицу

2) .

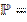
Задачи.

1) Пусть - цепь Маркова. Показать, что тоже цепь Маркова.

2) независимые одинаково распределенные целочисленные случайные величины с известными вероятностями Какой вид имеет матрица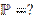

Лекция 14 (7.12.10)

Зададимся следующим вопросом: верно ли, что для однородных марковских цепей справедливо равенство

при всех натуральных k?

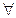
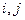Утверждение: однородная ЦМ , при всех .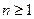

Доказательство: индукцией по .

База: - равенство следует из определения однородной ЦМ.

Пусть верно для , докажем для .

Рассмотрим

= = = = = = = = = .

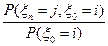Введем обозначение: 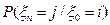- это переходная вероятность из состояния в состояние за шагов.

– это тоже стохастическая матрица (оба свойства выполняются).

Пусть известна 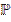- матрица переходных вероятностей за 1 шаг.

Как найти 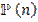- матрицу переходных вероятностей за шагов?

Поиск по сайту: