Теорема (Пуассона)

Будем рассматривать серии независимых испытаний Бернулли.

Пусть ₁₁ – серия из одного испытания с вероятностью успеха ;

₂₁ , ₂₂ – серия из двух независимых испытаний с вероятностью успеха в каждом из них ;

….

_n1 , …, _nn – серия из n независимых испытаний с вероятностью успеха в каждом из них ;

Обозначим . Тогда для фиксированного числа 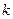справедливо соотношение:

Следствие: Пусть . Тогда 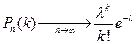для любого фиксированного .

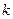Доказательство (теоремы):

Будем пользоваться следующими 3-мя простыми утверждениями, которые встречались в курсе математического анализа:

Утв.1 равномерно для

Утв.2 для любого фиксированного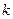

Утв.3 для любых

Рассмотрим только те , которые удовлетворяют неравенству .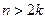

= =

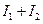
Теорема будет доказана

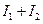
Из утв.2 следует: :

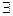
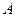Множество всех 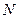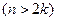разобьем на 2 непересекающихся подмножества:

Пусть 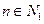, если , , 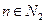если .

Не ограничивая общности, предположим, что оба эти подмножества счётные.

,будем оценивать и (по 3 утв.)

. Тогда

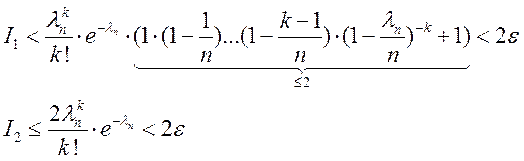
Показали, что при 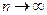+ может быть сколь угодно маленькой.

Примеры (применения трёх теорем).

1. Есть 1460 аспирантов и студентов. Р(хотя бы у одного День Рождения 1 января)=?

Рассматриваем случай не високосного года. Проводим опрос: ответ «Да»-успех, «Нет»-неудача.

Р(хотя бы у одного ДР 1 января)= (т. Пуассона)

2. Есть 1600 студентов и аспирантов. Какова вероятность, что у 420 человек ДР приходится на летний период?

Пусть все сезоны одинаковы по длительности По локальной теореме Муавра-Лапласа

А какова вероятность, что у 400 человек ДР приходится на летний период?

3. Количество людей, у которых ДР летом, не больше 420.

Поиск по сайту: