Определение. Дисперсией случайной величины называется число

Дисперсией случайной величины называется число

, (1)

если это число существует.

Справедливо также следующая запись:

Таким образом, дисперсия – это среднее квадратичного отклонения случайной величины от своего среднего.

Свойства дисперсии:

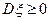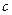1. , для некоторого (т.е. случайная величина с вырожденным распределением)

2.

3.

4. 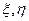- независимые случайные величины . Верно и для попарно независимых случайных величин (доказательство по индукции).

Замечание: Свойство 4 в обратную сторону неверно.

Доказательство свойств: 1. 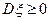, т.к. вычисляем

(неотрицательная функция интегрируется по вероятностной мере)

.

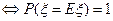2. = =

.

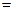
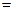
3. .

4. +

+ = {где и 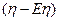независимы, т.к. и - независимы} = = {где =0 и =0} =

= .

Поиск по сайту: