Моменты случайной величины

Пусть на некотором вероятностном пространстве .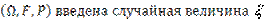

Пусть .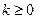

Определения:

1. Моментом 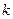-го порядка случайной величины наз. число , если это число существует.

2. Число наз. центральным моментом 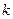-го порядка случайной величины .

3. Число 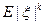наз. абсолютным моментом 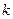-го порядка случайной величины .

4. Число 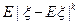наз. центральным абсолютным моментом 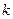-го порядка случайной величины .

Замечание. Все определенные моменты либо одновременно существуют, либо отсутствуют.

Свойства моментов:

1) Пусть 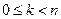и существует 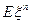. Тогда существует и .

Доказательство. Всегда справедливо неравенство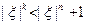

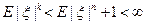
2) Неравенство Гельдера:

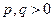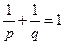
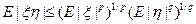: для любых случайных величин 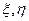(если их моменты существуют).

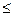
Доказательство. В курсе математического анализа для интегралов было неравенство 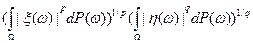(неравенство Гельдера для интегралов)

2’) Неравенство Коши – Буняковского – Шварца ():

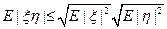
3) Неравенство Ляпунова ():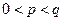

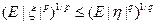
Иначе: введем функцию 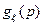- не убывает.

Доказательство. Имеет место равенство 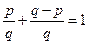. Воспользуемся неравенством Гельдера:

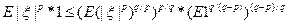= {где = 1} =

Проблема моментов. Пусть имеется набор чисел

Существует ли такая случайная величина , что ? И если существует, то она единственная?

Существует несколько различных теорем, в которых даются условия решения этой задачи. Приведем одно из условий.

Проблема моментов разрешима единственным образом, если

.

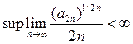Пусть имеется случайных величин 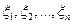, определенных на одном и том же вероятностном пространстве .

Обозначим случайный вектор .

Пусть , .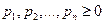

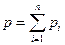Определение:

Число называется смешанным моментом порядка случайных величин .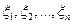

Замечание: Если для всех существует 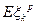(момент порядка ), то существует и смешанный момент порядка для - .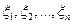

Доказательство. 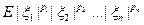≤ 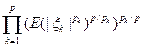= { по неравенству Гельдера}=

= .

Рассмотрим .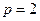

Определения:

1. Обозначим 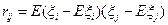- ковариация случайных величин 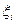и .

2. Составим матрицу 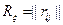. Это ковариационная матрица случайного вектора .

Пусть далее

- матрица, составленная из случайных величин . Определим .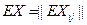

Рассмотрим случайный вектор .

Тогда 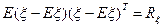, где 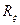- ковариационная матрица.

Свойства ковариационной матрицы :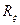

1) - не случайный вектор .

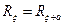Доказательство.

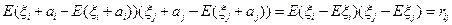
2) 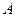- не случайная матрица

Доказательство.

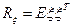Предположим, что , и в этом случае . Понятно, что

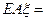
Замечание.

Пусть 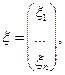- независимы. Тогда .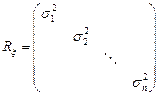

Поиск по сайту: