Случайные величины с абсолютно непрерывным распределением

Определение:

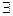
- с абсолютно непрерывным распределением , где - функция, которую будем называть плотностью распределения случайной величины .

В частности, если , то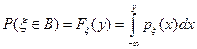

Таким образом, 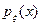= почти всюду.

Свойства :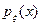

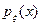
1. почти всюду

2. =1

Примеры (наиболее распространенных случайных величин с абсолютно непрерывным распределением)

1) - с равномерным распределением на ;

Обозначение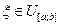

Это означает, что: плотность

График функции распределения:

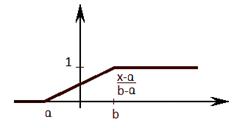
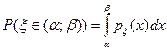
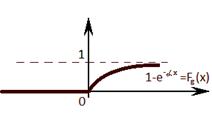
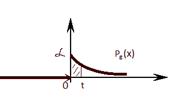
2) - с экспоненциальным распределением с параметром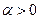

Это означает, что: плотность

График функции распределения:

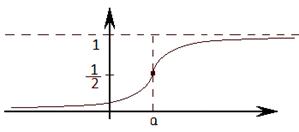
3) - с нормальным (гауссовским) законом распределения с параметрами , , 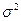где , .

Обозначение: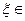

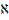
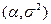
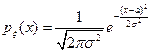
Если , - со стандартным нормальным распределением.

При этом

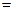
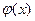
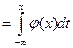
Графики плотности и функции распределения:

4) - с распределением Коши.

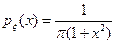
Графики:

плотность функция распр.

3.Сингулярные случайные величины – те, у которых функция распределения непрерывна, но ее производная почти всюду равна 0.

Поиск по сайту: