Определение 3

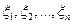- независимые случайные величины - независимые 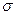- алгебры.

(Напомним, что означает что σ-алгебры являются независимыми:

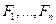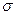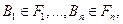
-независимые - алгебры. 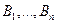- независимые случайные события.)

Примеры.

1. Пусть в качестве Ω выступает множество точек квадрата со стороной 1, т.е.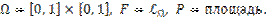

Независимы л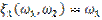и: и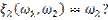

Рассмотрим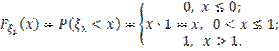

Теперь рассмотрим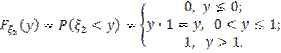

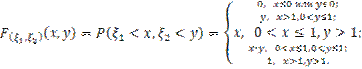
Видим, что 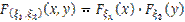, т. е. наши случайные величины независимы.

Независимы л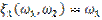и: и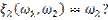

Имеем

.

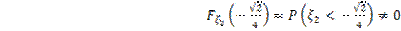Случайные величины зависимы.

Рассмотрим случай, когда случайный вектор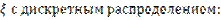

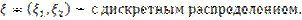
Теорема. Пусть 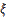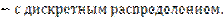Тогда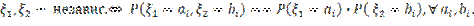

Док. «» Необходимость.

Если случайные величины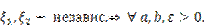

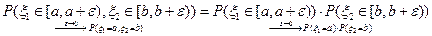
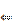«» Достаточность.

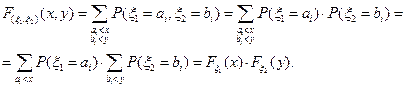
Теорема: Пусть - случайные величины с абсолютно непрерывным распределением. Тогда - независимые случайные величины 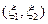- с абсолютно непрерывным распределением и его плотность распределения .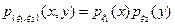

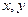Лекция 8. (26.10.10)

Теорема: Пусть - независимые случайные величины. Если при всех 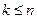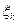- с абсолютно непрерывным распределением, то 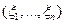- с абсолютно непрерывным распределением и плотность случайного вектора имеет вид: .

Доказательство. 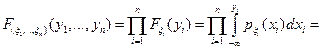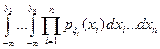, где

.

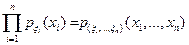Теорема: Пусть - независимые случайные величины, 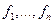- измеримые функции 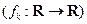. Тогда 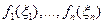- независимые случайные величины.

Док-во. Пусть 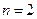(для n>2 доказательство проводится точно так же).

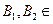
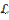
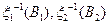- независимые - независимые события.

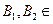
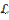
- измеримые подмножества прямой.

.

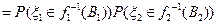
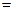
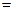
Поиск по сайту: