Распределение суммы независимых случайных величин. Свертка функций распределения

Пусть 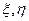- независимые случайные величины с известными нам функциями распределения .

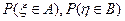И пусть мы знаем значения . Как вычислять ?

Известно, что = . Следовательно, нам надо научиться находить .

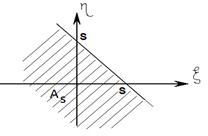Рассмотрим случайный вектор , знаем его функцию распределения = {где - произвольная точка} =

= =

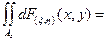
Вычисляем это как повторный интеграл: = =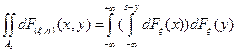

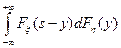
Итак, получаем формулу для вычисления функции распределения суммы независимых случайных величин, которую называют формулой свертки:

Формула свертки для функции распределения:

= (*)

Следствия:

1) Пусть - с абсолютно непрерывным распределением (имеется 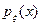- плотность).

Тогда - с абсолютно непрерывным распределением и = . Это получается из формулы (*) дифференцированием по x.

2) Если , - независимые случайные величины с абсолютно непрерывным распределением,

то - с абсолютно непрерывным распределением и = =

=

(Последняя формула называется формулой свертки для плотностей.)

Поиск по сайту: