 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Случайные события, операции над событиями, вероятность, вероятностные пространства
Будем рассматривать эксперимент, который заканчивается одним из многих исходов. Мы можем описать все возможные исходы, но каким конкретно исходом закончится эксперимент, заранее мы сказать не можем. Введём ряд определений и обозначений.
 -множество исходов нашего эксперимента (множество элементарных событий);
-множество исходов нашего эксперимента (множество элементарных событий);
 -элементарные события, элементы множества исходов;
-элементарные события, элементы множества исходов;
Пусть на  определена
определена  - σ -алгебра подмножеств
- σ -алгебра подмножеств  ;
;
Если 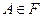
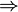
 – случайное событие.
– случайное событие.
Будем говорить, что событие 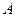 произошло, если эксперимент заканчивается исходом
произошло, если эксперимент заканчивается исходом 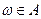 , если
, если 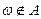 – не произошло.
– не произошло.
Рассмотрим 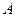 и
и  -случайные события (
-случайные события ( )
) 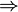
 – сумма событий
– сумма событий 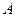 и
и  ;
;
Примеры случайных событий.
Рассмотрим однократное подбрасывание игрального кубика:  = {
= { 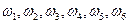 }
}
Если множество  конечное или счётное, то в качестве σ –алгебры будет множество всех подмножеств (если n элементов, то в σ –алгебре 2ⁿ событий)
конечное или счётное, то в качестве σ –алгебры будет множество всех подмножеств (если n элементов, то в σ –алгебре 2ⁿ событий)
С={  }-выпала чётная грань, D= {
}-выпала чётная грань, D= {  }-выпала грань, делящаяся на 3.
}-выпала грань, делящаяся на 3.
Пусть 
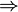
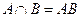 - произведение случайных событий
- произведение случайных событий 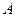 и
и  ;
;
 - событие, обратное к событию
- событие, обратное к событию 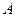 .
.

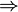
 - достоверное событие, событие, которое всегда происходит.
- достоверное событие, событие, которое всегда происходит.
 = Ø - невозможное событие.
= Ø - невозможное событие.
Пусть имеются два случайных события 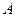 и
и  (
( ) и
) и  . Тогда события
. Тогда события 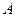 и
и  называют несовместными событиями. Например,
называют несовместными событиями. Например, 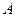 и
и  – пара несовместных событий.
– пара несовместных событий.
Рассмотрим набор событий  , для которых выполнены 2 условия:
, для которых выполнены 2 условия:
1. 
2. 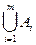 =
=  -достоверное событие
-достоверное событие
Тогда 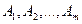 – полная система событий.
– полная система событий.
Ещё один пример.
Рассмотрим отрезок [0,1]. Случайно «бросаем» на него точку. Тогда  . Множество точек на отрезке более чем счётно. В качестве σ- алгебры
. Множество точек на отрезке более чем счётно. В качестве σ- алгебры  берут множество измеримых по Лебегу подмножеств.
берут множество измеримых по Лебегу подмножеств.
Определим основное понятие «вероятность»:
Пусть имеются  . Функция
. Функция 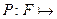
 удовлетворяет 3 условиям:
удовлетворяет 3 условиям:
1) 

2) 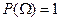
3) Не более чем счётное число случайных событий 
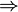
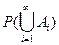 =
= 
В этом случае  называется вероятностью, а три условия - аксиомами.
называется вероятностью, а три условия - аксиомами.
Тройка элементов  – вероятностное пространство.
– вероятностное пространство.
Пример.
1. Однократное подбрасывание монеты.
О - орёл, Р - решка.
Ω={O, Р},  ={{O}, {P}, {O,P},Ø}.
={{O}, {P}, {O,P},Ø}.
 ({O})=
({O})=  ({P})=⅟₂,
({P})=⅟₂,  (Ω)=1,
(Ω)=1,  (Ø)=0;
(Ø)=0;
 ({O})=⅕,
({O})=⅕,  ({P})=⅘,
({P})=⅘,  (Ω)=1,
(Ω)=1,  (Ø)=0.
(Ø)=0.
Чёткого способа задания нет. Но если есть симметрия, то пользуемся ей.
2. Дважды подбрасываем игральный кубик.
Ω = {(i, j): 1≤ i, j ≤ 6}. Всего 36 возможностей.
F=  .
.
Будем предполагать, что кубики правильные - честные.
 ({(i,j)})=⅟₃₆;
({(i,j)})=⅟₃₆;  ({
({  })=k⁄₃₆.
})=k⁄₃₆.
Поиск по сайту: