Математическое ожидание случайной величины

Пусть на некотором вероятностном пространстве : Ω→R,

Определение

Математическим ожиданием случайной величины называют число , вычисляемое по формуле , если оно (это число) существует. {Если интеграл расходится, то говорят, что у случайной величины отсутствует математическое ожидание}

Рассмотрим 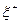=max и =min .

Существование эквивалентно существованию 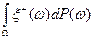и .

Тогда имеем

= +

= -

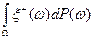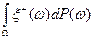Таким образом, существование эквивалентно существованию .

Что вообще означает число ?

Рассмотрим следующий пример: пусть с дискретным распределением:

			…
			…

Введем случайное событие ;

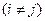, то есть эти события несовместны. Кроме того, .

Тогда

= , где = = .

Замечание. Математическое ожидание часто еще называют средним случайной величины.

Давайте теперь предположим, что значений у случайной величины 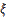ровно . И все - среднее случайнойвеличины. Это еще одно пояснение, почему математическое ожидание называют средним случайной величины.

Итак, далее будем считать, что математическое ожидание и среднее случайной величины – синонимы.

Свойства

1.

2. Линейность математического ожидания.

3.

4.

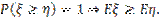
Доказательство свойства 4: P()=1

5.

Доказательство свойства 5:

.

Теорема. Пусть

вероятностном пространстве;

Поиск по сайту: