Математическое описание импульсных систем

Если непрерывные процессы описываются обыкновенными дифференциальными уравнениями, то для описания дискретных процессов используются разностные уравнения.

Разностным уравнением называется уравнение, связывающее ординаты решетчатой функции с их конечными разностями. Значения решетчатой функции времени f (nT) или в сокращенной форме f (n) определяются в дискретные моменты времени t = nТ, где n – целое число, а Т – период повторения. Операция замены непрерывной функции f (t)решетчатой функцией f (n) = f (t)| _t=nT показана на рис. 4.5.

Рис. 4.5. Решетчатая функция

Ординаты решетчатой функции представляют собой так называемые дискреты исходной непрерывной функции f (t) при t = nТ. Дискреты f (t) могут быть определены и для смещенных моментов времени t = nТ + D Т = (n + e) Т, e = D Т/Т < 1. Смещенная решетчатая функция обозначается f (n + e).

По определению, первая прямая (восходящая) разность или разность первого порядка имеет вид

D x (n) = x (n +1) – x (n).

Вторая разность или разность второго порядка – это разность первых разностей. Поэтому

D² x (n) = D x (n +1) – D x (n) = x (n +2) – 2 x (n +1) + x (n).

В общем случае имеем

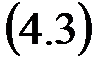
Первая обратная (нисходящая) разность имеет вид

Ñ x (n) = x (n) – x (n –1).

Обратная разность второго порядка

Ѳ x (n) = Ñ x (n) – Ñ x (n –1) = x (n) – 2 x (n –1) + x (n –2).

В общем случае

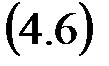
Разностное уравнение может быть записано в прямой или обратной разностной формеилив соответствующих формах смещенных решетчатых функций.

При использовании прямых разностей неоднородные линейные разностные уравнения имеют вид

b ₀D ^my (n) + b ₁D ^{m -1} y (n) + …+ b _m y (n) = f (n),

где f (n) – заданная, а y (n) – искомая решетчатые функции.

С учетом выражений для прямых разностей получим

a ₀ y (n+m) + a ₁ y (n+m– 1) + …+ a _m y (n) = f (n).

Соответствующие уравнения при использовании обратных разностей имеют следующий вид

b ₀Ñ ^my (n) + b ₁Ñ ^{m -1} y (n) + …+ b_my (n) = f (n).

a ₀ y (n) + a ₁ y (n– 1) + …+ a _m y (n–m) = f (n).

Пример. Решить уравнение D² y (n) + 2D y (n) + 2 y (n) = 1(n) с начальными условиями y (0) = 1, y (1) = 0.

D² y (n) + 2D y (n) + 2 y (n) = y (n +2) – 2 y (n +1) + y (n) + 2 y (n +1) – 2 y (n) + 2 y (n) = 1(n)

y (n +2) + y (n) = 1(n); y (n +2) = 1(n) – y (n)

n = 0: y (2) = 1 – y (0) = 1 – 1 = 0 n = 1: y (3) = 1 – y (1) = 1 – 0 = 1

n = 2: y (4) = 1– y (2) = 1 – 0 = 1 n = 3: y (5) = 1– y (3) = 1 – 1 = 0

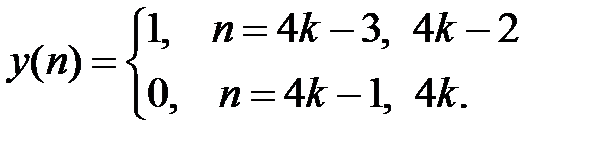
Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие по уравнению вида (4.1) вычислять значения y (m+n) при n = 0, 1, 2,… при заданных начальных условиях y (0), y (1),..., y (m– 1). Такие вычисления легко алгоритмизировать даже в случае, когда коэффициенты разностных уравнений а_i (i = 0, 1,..., m) с течением времени изменяются. Это отличает разностные уравнения от их непрерывных аналогов – дифференциальных уравнений.

Для определения и исследования решений разностных уравнений широко используются дискретное преобразование Лапласа, Z -преобразование, w -преобразование, а также частотные методы.

4.1.2 Z- преобразование

Для решетчатых функций времени вводится понятие дискретного преобразования Лапласа

Изображение решетчатой функции F *(p) является функцией величины e^pT.

Для исследования импульсных систем используется Z- преобразование, которое связано с дискретным преобразованием Лапласа. Под Z- преобразованием понимается изображение несмещенной решетчатой функции, определяемое формулой

Для Z- преобразования используется обозначение F (z) = Z [ f (n)],
где Z – оператор преобразования, z – аргумент преобразования. Операцию Z-преобразования распространяют на производящую функцию f (t) и преобразование Лапласа F (p) производящей функции:

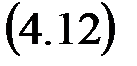F (z) = Z [ f (t)] или F (z) = Z [ F (p)],

при этом Z [ f (t)] = Z [ f (n)], t = nT; Z [ F (p)] = Z [ f (n)], f (n) = f (t), t = nT,
f (t) = L ^-1{ F (p)}.

Для смещенных решетчатых функций используется модифицированное Z-преобразование

Обозначается оно как F (z,e) = Z _e[ f (n)], Z _e[ f (t)], или Z _e[ F (p)].

Z -преобразованиепрактически совпадает с дискретным преобразованием Лапласа и отличается от него только изображением аргумента, z = e^pT.

Отметим несколько важных свойств Z -преобразования.

а. Линейность

Z [ c ₁ f ₁(n) + c ₂ f ₂(n)] = c ₁ F ₁(z) + c ₂ F ₂(z).

б. Правило упреждения или запаздывания

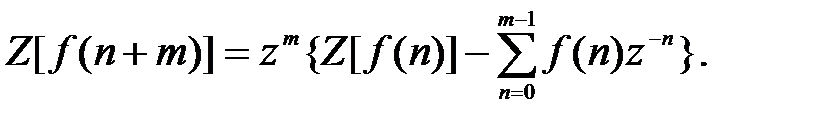
При нулевых начальных условиях f (0) = f (1) =…= f (m –1) = 0

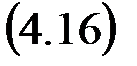Z [ f (n+m)] = z^mZ [ f (n)] = z^mF (z).

с. Правило умножения на аргумент

Это правило позволяет вычислять Z -преобразование (изображение) полиномиальных решетчатых функций.

д. Правило свертки. Если F ₁(z) = Z [ f ₁(n)] и F ₂(z) = Z [ f ₂(n)], то

е. Конечные значения. Начальные и конечные значения решетчатой функции определяются в виде

Примеры вычисления Z–преобразования

Рис. 4.6. Примеры решетчатых функций

1. f (n) = 1(n) (рис. 4.6, а)

По определению Z -преобразования

2. f (n) = nT (рис. 4.6, б).

Используя правило умножения на аргумент, найдем

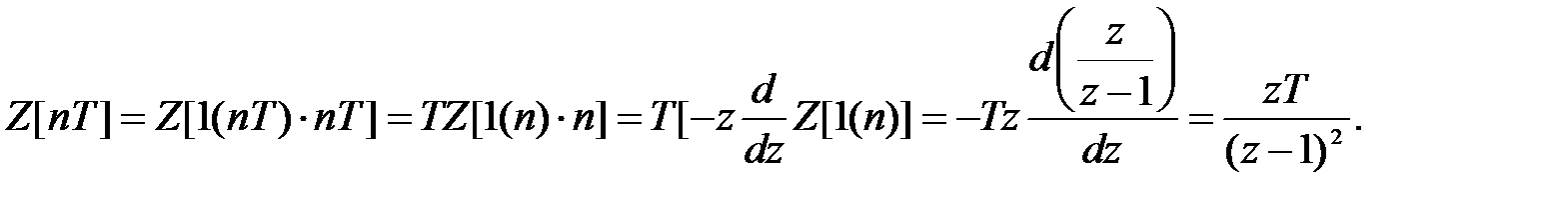
Для смещенной импульсной функции f (n +e) = (n +e) T модифицированное преобразование дает

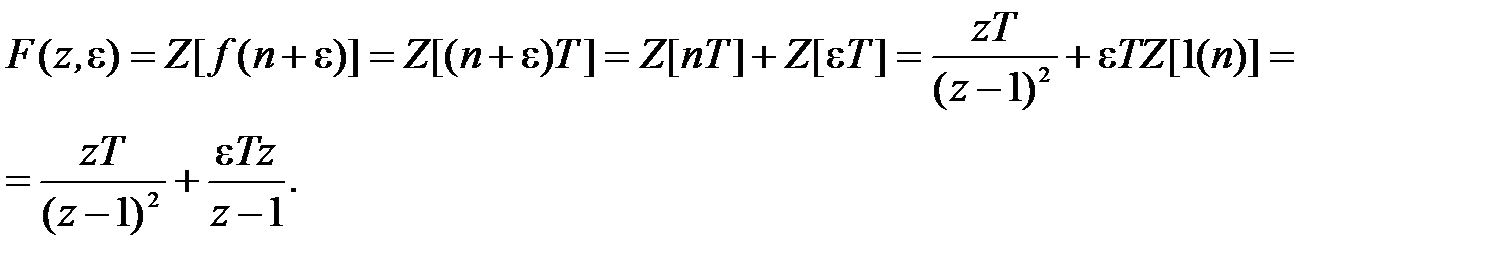
3. f (n +e) = e ^{-g( n +e) T} _.

По определению, Z -преобразования

Обозначим d = e ^{-g T}:

Для действительных g = a и d = e ^{–a T} (рис. 4.6, в) Z -преобразование имеет вид

Если g = a + i b комплексное число, то импульсная функция примет вид

f (n +e) = e ^{-a(n +e) Т} [ cos b(n +e) T – i∙sin b(n +e) T ]

Отделяя реальную и мнимую части изображения, запишем

Из этой формулы можно получить Z -преобразования основных функций (табл. 4.1). Например, импульсная функция f (nT) = sin b nT (рис. 4.5, г) получается из выражения f (nT) = f (n +e) =
e ^{-a(n +e) Т} [ cos b(n +e) T – i∙sin b(n +e) T ] при a = 0, d = 1, e = 0. Соответствующее ей Z -преобразование – есть мнимая часть полученного преобразования при a = 0, d = 1, e = 0, откуда

Таблица 4.1

Таблица Z-преобразований

f (t)	F (p)	f (n)	F (z)	F (z, e)
d(t)		d(n)
1(t)		1(n)
t	ё	nT

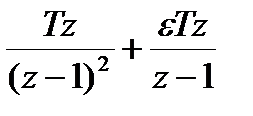
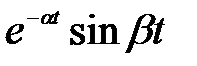
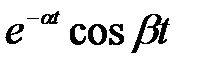
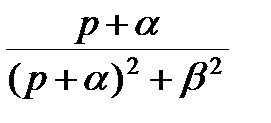
Решение разностных уравнений с помощью Z-преобразования

Рассмотрим разностное уравнение

a ₀ y (n+m) + a ₁ y (n+m– 1) + …+ a _m y (n) = f (n)

с начальными условиями y (k) = y_k, k = 0, 1,…, m– 1.

Найдем Z -преобразование от его левой и правой частей:

a ₀ Z { y (n+m)} + a ₁ Z { y (n+m– 1)} + …+ a_mZ { y (n)} = Z { f (n)}.

В соответствии с правилом смещения для случая упреждения на r тактов

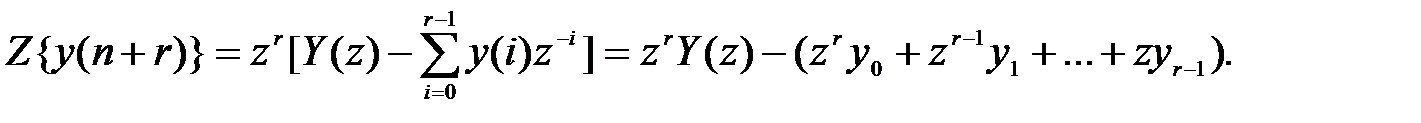
Подставляя r = m, m– 1, …, 0 и переходя в уравнении к изображениям, получим

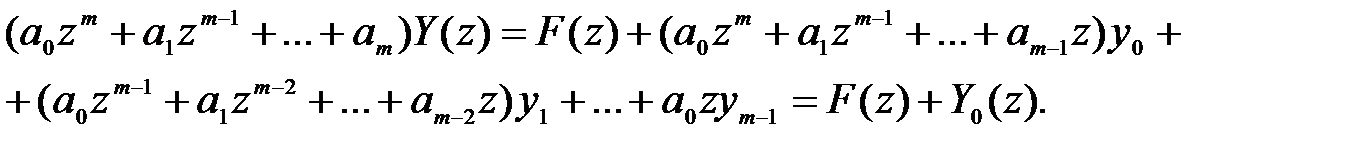
В правой части этого уравнения, кроме изображения F (z) решетчатой функции f (n), находятся члены, определяемые начальными условиями. Сумма их обозначена Y₀ (z). Изображение Y (z) искомой решетчатой функции y (n) примет вид

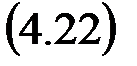
где

Отдельный интерес представляет случай, когда искомая решетчатая функция тождественно равна нулю до момента n = m –1 включительно, y (k) = 0, k = 0, 1,..., m– 1 (эквивалентно случаю нулевых начальных условий при решении дифференциальных уравнений для непрерывных функций). Тогда выражение (4.22) приобретает вид

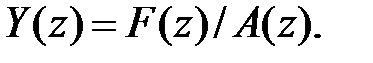
Остается найти оригинал y (n) = Z ^-1{ Y (z)}.

Существуют различные методы определения решетчатой функции по ее изображению: использование вычетов, рядов Лорана, таблиц Z -преобразования.

Пример. Решим разностное уравнение y (n +1) – y (n) = 1(n) с начальным условием y (0)=0.

Применим Z -преобразование к обеим частям уравнения и получим

Из таблиц Z -преобразования находим

Следовательно, y (n) = n.

Решить это уравнение легко, используя рекуррентное соотношение

y (n +1) – y (n) = 1(n).

Так как y (0) = 0, то y (1) = y (0) + 1 =1, y (2) = y (1) + 1 = 2 и т. д.

Поиск по сайту: