 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Синтез модального регулятора
Название «модальное управление» объясняется используемым в зарубежной литературе термином «мода» для обозначения отдельных составляющих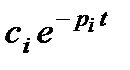 
свободного движения. Суть модального управления состоит в определении значений коэффициентов передачи безынерционных обратных связей по всем переменным состояния объекта (u = –k×x) с целью обеспечения заданного распределения корней характеристического уравнения замкнутой САУ.
Корни характеристического уравнения САУ полностью определяют устойчивость линейной системы. В свою очередь, корни однозначно зависят от коэффициентов уравнения, поэтому модальное управление можно трактовать как целенаправленное изменение коэффициентов характеристического уравнения объекта с помощью безынерционных ОС.
Из литературы известны стандартные виды характеристических полиномов 1-8 порядков и соответствующие им графики переходных процессов с указанными на них показателями качества (биномиальные полиномы Ньютона, полиномы Баттерворта и др.). Исходя из порядка объекта и заданных в техническом задании показателей качества САУ, можно выбрать требуемый график переходного процесса и соответствующий ему «стандартный» характеристический полином, а затем выполнить синтез модальных ОС, обеспечивающих заданные показатели качества САУ. Таким образом, теория модального управления позволяет осуществлять синтез многоконтурных замкнутых САУ с заранее заданными показателями качества.
Основные достоинства модального управления:
1. Синтезированная модальная САУ не требует проверки на устойчивость (так как она заранее должна быть устойчивой и обладать требуемыми запасами устойчивости).
2. Синтезированная модальная САУ не требует введения дополнительных корректирующих устройств (так как она сама уже удовлетворяет требуемым показателям качества).
3. Введение модальных ОС, в силу их безынерционности, не повышает порядок объекта и не нарушает его управляемость и наблюдаемость (что может произойти при введении пассивных инерционных корректирующих устройств).
4. Техническая реализация модальных САУ осуществляется относительно просто и экономично с помощью маломощных измерительно-преобразовательных устройств и электронных усилителей.
Рассмотрим методику синтеза модальных регуляторов.
3.5.1 Синтез для случая полностью управляемого объекта
с одним входом
Уравнение полностью управляемого объекта с одним входом имеет вид:
, 
.
Требуется определить коэффициенты передачи 
модального регулятора
,
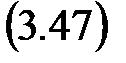
при которых замкнутая САУ имела бы желаемый «стандартный» характеристический полином
Q *(p) = pn + g 1 pn -1 + … + gn- 1 p + gn.
1. Определяем характеристический полином Q (p) матрицы A
Q (p) = | p E – A | Þ pn + q 1 pn -1 + … + qn- 1 p + qn.
2. Вычисляем коэффициенты передачи регулятора в каноническом базисе, которые записываются в виде вектор-строки
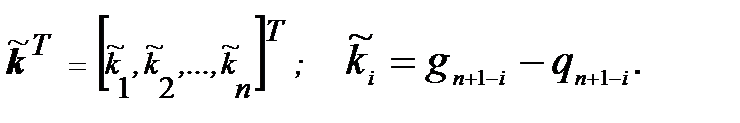
Элементы вектора 
определяются как разности соответствующих коэффициентов желаемого характеристического полинома Q *(p) и характеристического полинома Q (p) матрицы A: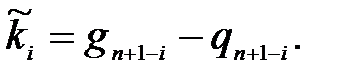 
3. Составляем матрицу управляемости R в исходном базисе
.
4. Для полинома Q (p) составляем каноническую пару 
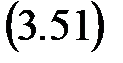
5. Составляем матрицу управляемости 
в каноническом базисе
.
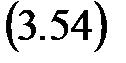
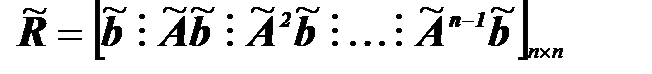6. Вычисляем матрицу преобразования P
7. Вычисляем вектор-строку коэффициентов передачи регулятора в исходном базисе k T
Для проверки полученного решения задачи целесообразно вычислить матрицу G = A – bk T и определить ее характеристический полином
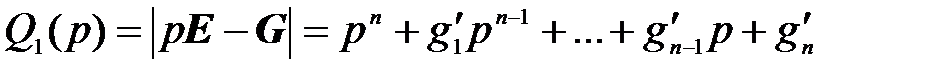
Совпадение коэффициентов этого полинома с соответствующими коэффициентами желаемого полинома (3.47) указывает на правильность решения задачи.
Указанный алгоритм легко реализуется для вычислений на компьютере на базе стандартных программ матричной алгебры.
Пример 1. Заданы структурная схема и параметры объекта (рис. 3.22).
Рис. 3.22. Структурная схема объекта
Корни характеристического уравнения данного объекта
p 1 = –1/ T 1 = –2; p 2 = –1/ T 2 = –1, следовательно, степень его устойчивости η = 1. Требуется определить коэффициенты обратных модальных связей k 1, k 2, обеспечивающие желаемые значения корней p 1 = p 2 = –3 и соответствующую им степень устойчивости η = 3 замкнутой системы.
Уравнения звеньев объекта
Отсюда
при этом матрицы A и b уравнения (3.45) имеют вид
Далее действуем согласно приведенному выше алгоритму.
1. Определяем согласно (3.48) характеристический полином Q (p) матрицы A
Q (p) = | p E – A | = 
Þ q 1 = 3, q 2 =2.
2. Определяем согласно (3.47) желаемый характеристический полином Q* (p)
Q* (p) = (p – p 1)(p – p 2) = (p + 3)(p + 3) = p 2 + 6 p + 9 Þ g 1 = 6, g 2 =9.
3. Вычисляем коэффициенты передачи регулятора в каноническом базисе согласно (3.49)
.
4. Составляем матрицу управляемости R в исходном базисе согласно (3.50)
.
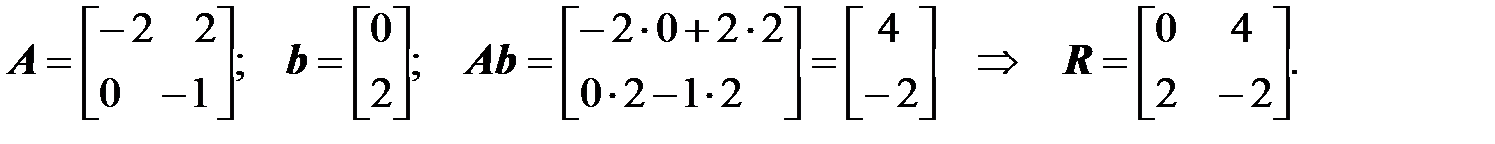
5. Для полинома Q (p) составляем каноническую пару 
согласно (3.51)
6. Составляем матрицу управляемости 
в каноническом базисе согласно (3.52)
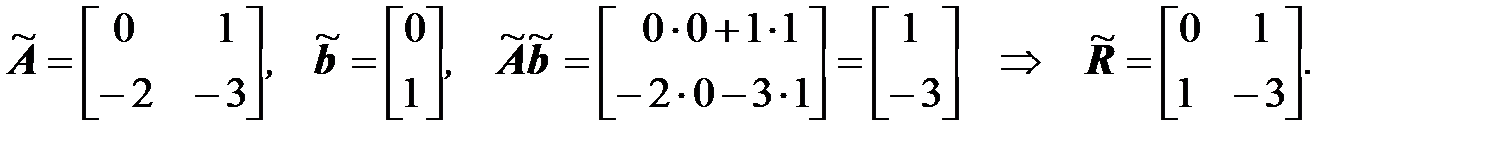
7. Вычисляем матрицу преобразования P согласно (3.53)
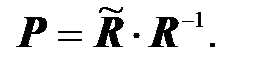
8. Вычисляем вектор-строку коэффициентов передачи регулятора в исходном базисе k T согласно (3.54)
Итак, k 1 = 0,25; k 2 = 1,5.
Выполним проверку. Согласно (3.55) вычисляем G = A – bk T
Тогда
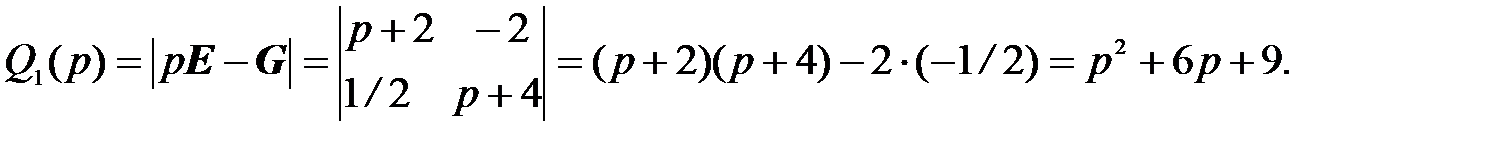
Полученный характеристический полином замкнутой модальной системы совпадает с указанным ранее желаемым полиномом Q* (p), следовательно, коэффициенты k 1, k 2 определены правильно.
Безынерционные модальные обратные связи изменяют общий коэффициент передачи системы и тем самым влияют на установившееся значение выходной переменной объекта. Чтобы исключить такое влияние, достаточно на входе системы (рис. 3.22) установить безынерционный усилитель, коэффициент усиления k y которого определяется из условия равенства коэффициента усиления K замкнутой модальной САУ и коэффициента усиления k 0самого объекта:
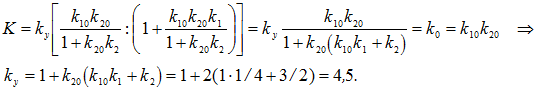
Поиск по сайту: