Передаточные функции типовых импульсных звеньев

1. Идеальный импульсный дифференциатор (разностный анализатор), y (n) = D x (n).

Из определения прямой разности D x (n) = x (n +1) – x (n) получаем уравнение y (n) = x (n +1) – x (n). Переходя к операторной форме

Y (z) = zX (z) – X (z),

определяем передаточную функцию

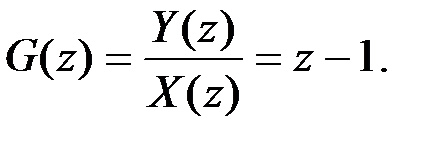
2. Реальный импульсный дифференциатор, y (n) = Ñ x (n).

Как и в предыдущем примере, получаем

Ñ x (n) = x (n) – x (n –1) Þ y (n) = x (n) – x (n –1) Þ Y (z) = X (z) – z ^–1 X (z)

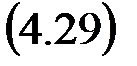
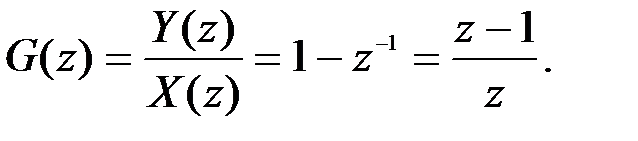
3. Идеальный сумматор, y (n) = .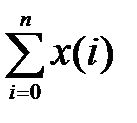

Пользуясь определением идеального сумматора, y (n) = 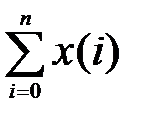, составим прямую разность

D y (n) = y (n +1) – y (n) = x (n +1).

Применяя правило смещения аргумента, найдем операторную форму уравнения y (n +1) – y (n) = x (n +1)

(z –1) Y (z) = zX (z)

и передаточную функцию идеального сумматора

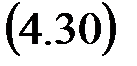
4. Реальный сумматор y (n) =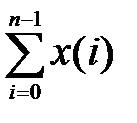

Реальный сумматор можно записать в виде 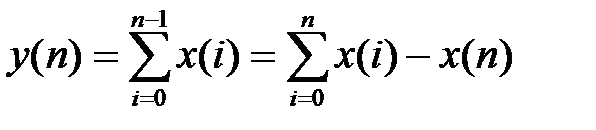. Тогда, используя передаточную функцию идеального сумматора, найдем

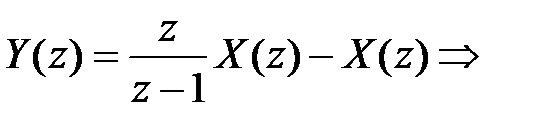
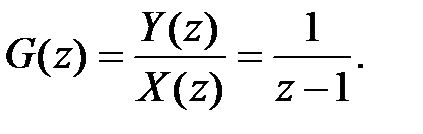
5. Сдвигающее звено

Сдвиг импульсной функции на r периодов описывается разностным уравнением y (n) = x (n ± r) и передаточной функцией

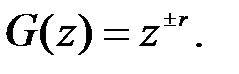
Поиск по сайту: