Частотные характеристики соединения звеньев

– Последовательное соединение

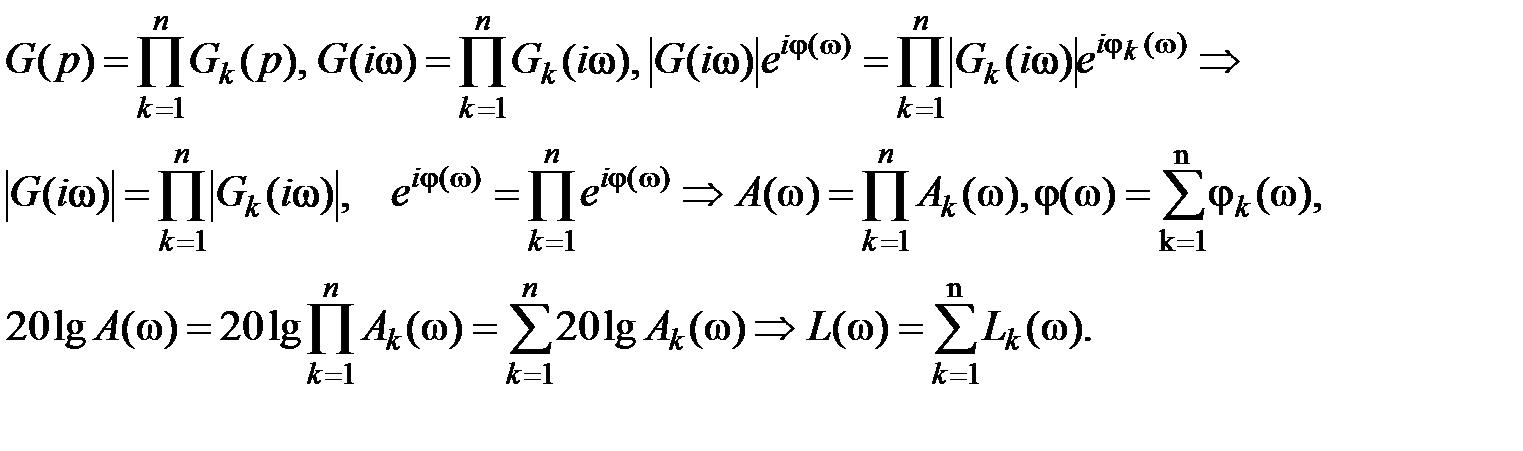
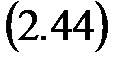
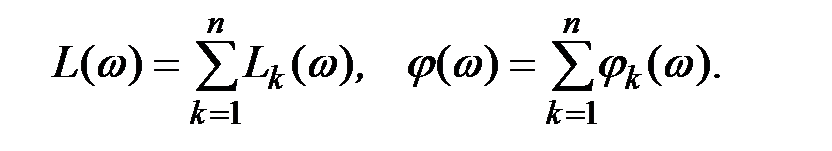
– Параллельное соединение

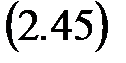
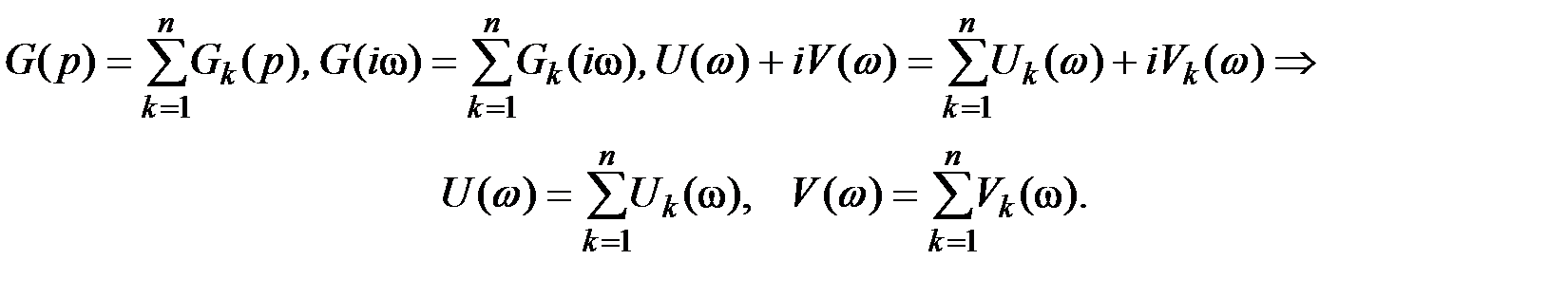– Соединение с обратной связью

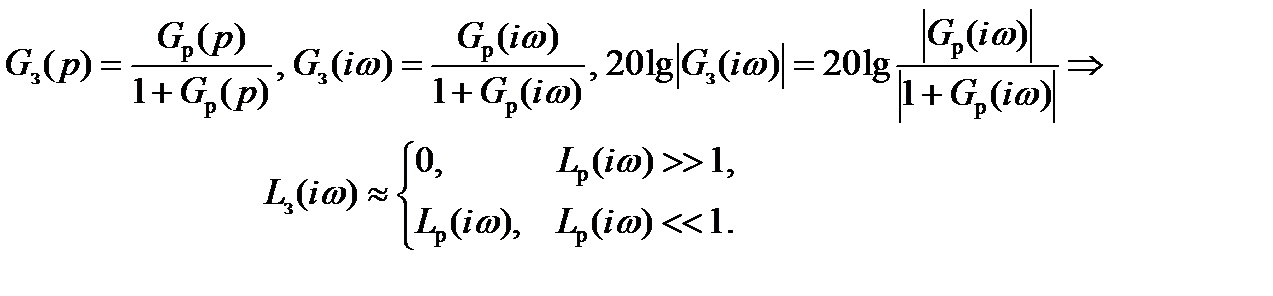
2.3.5 Построение логарифмических частотных характеристик
сложных систем

Логарифмические частотные характеристики сложных систем могут быть вычислены суммированием соответствующих характеристик элементарных звеньев (систем 1-го и 2-го порядка). Действительно, передаточная функция линейной системы представляет собой отношение двух полиномов от p: G (p) = P (p)/ Q (p), каждый из которых может быть разложен на множители. Звенья 1-го порядка соответствуют действительным корням, звенья 2-го порядка – комплексно сопряженным корням, могут также быть чисто нулевые корни. Следовательно,

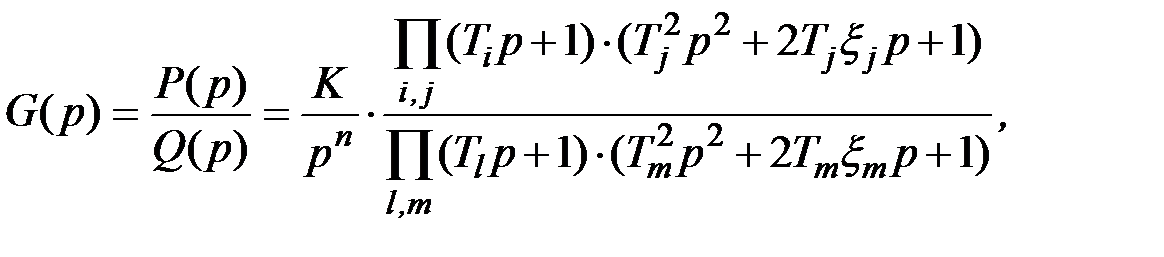
где G_i (p) – ПФ отдельных (элементарных) звеньев: усилителя, интегратора, апериодического, колебательного, дифференцирующего и т. д.

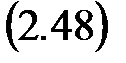
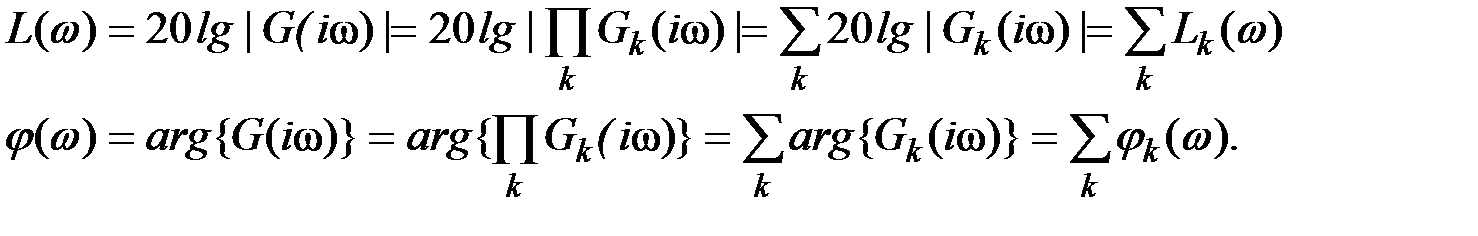
Правила приближенного построения логарифмических частотных характеристик (асимптотических ЛАХ, ЛФХ)

При приближенном построении ЛАХ и ЛФХ используются асимптотические свойства указанных характеристик элементарных звеньев. Последовательность построения:

1. Привести ПФ G (p) к стандартной форме – в виде произведения ПФ элементарных звеньев.

2. Рассчитать значения сопрягающих частот w _i, которые определяются как величины обратные постоянным времени звеньев w _i = 1/ T_i. Расположить полученные значения частот в порядке возрастания: w₁ – наименьшая сопрягающая частота, w₂ – следующая по величине и т. д.

3. Выбрать масштаб и нарисовать координатные оси. На оси абсцисс отложить значения сопрягающих частот и через эти точки провести вертикальные линии.

4. Построение ЛАХ начать с ее низкочастотной асимптоты. При w<<w₁ поведение системы определяется наличием идеальных интегрирующих и дифференцирующих звеньев (G (p) =1/ p, p), так как в этой области значения ЛАХ всех элементарных звеньев, кроме указанных, асимптотически стремятся к нулю. С учетом того, что для одного интегратора ЛАХ имеет угол наклона к оси абсцисс
–20 дБ/дек, получаем что угол наклона низкочастотной асимптоты составляет –20∙ n дБ/дек, где n – число интеграторов. Прямая с этим наклоном должна проходить при w = 1 через точку с ординатой 20 lg k, где k – общий коэффициент усиления системы. Отметим, что при отсутствии интегрирующих и дифференцирующих звеньев низкочастотная часть графика представляет собой горизонтальную линию, проходящую на уровне 20 lg k. Если же при записи передаточной функции в стандартной форме окажется, что множитель вида pⁿ находится в числителе (дифференцирующие звенья), а не в знаменателе, то угол наклона прямой будет +20∙ n дБ/дек.

5. После каждой сопрягающей частоты w_i изменить угол наклона асимптотической ЛАХ по сравнению с тем наклоном, который она имела до рассматриваемой частоты, в зависимости от того, какому элементарному звену эта частота соответствует: наклон изменяется на –20 дБ/дек (вниз на 20 дБ/дек) в случае инерционного звена (1-го порядка); –40 дБ/дек – колебательного звена (2-го порядка); +20 дБ/дек (вверх на 20 дБ/дек) для дифференцирующего звена 1-го порядка и +40 дБ/дек для дифференцирующего звена 2-го порядка.

6. Фазовая характеристика в низкочастотной области (w << w₁) при отсутствии неустойчивых звеньев равна –p/2∙ n или 0. При наличии неустойчивых (неминимально фазовых) звеньев следует учесть фазовый сдвиг, соответствующий этим звеньям при w = 0. Например, для неустойчивого апериодического звена G (p) = 1/(Tp -1) – j(0) = -p, для неустойчивого колебательного звена
G (p) = 1/(T ² p ²-2 T x p +1): j(0) = 0.

7. Для построения асимптотической ЛФХ при отсутствии неустойчивых звеньев достаточно использовать формулу j(w) = p/40× dL / dlg w и учесть, что каждый излом L (w) дает разрыв: –p/2 – для инерционного звена, –p – для колебательного, +p/2 – для дифференцирующего 1-го порядка и +p – для дифференцирующего
2-го порядка. При наличии неминимально фазовых звеньев приведенной формулой пользоваться нельзя и следует суммировать фазовые характеристики отдельных звеньев.

Пример.

Построить логарифмические частотные характеристики системы

Рис. 2.32. Структурная схема

Логарифмические частотные характеристики имеют вид

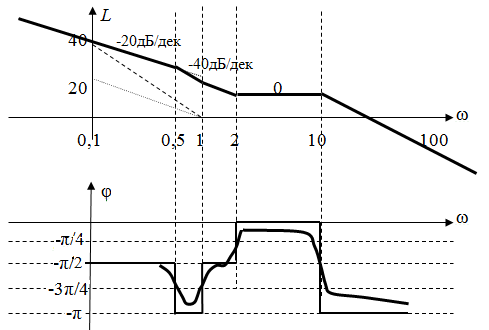
Рис. 2.33. Логарифмические частотные характеристики

Тест (15 мин)

1. Система описывается дифференциальными уравнениями. Необходимо построить структурную схему и найти передаточную функцию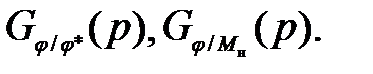

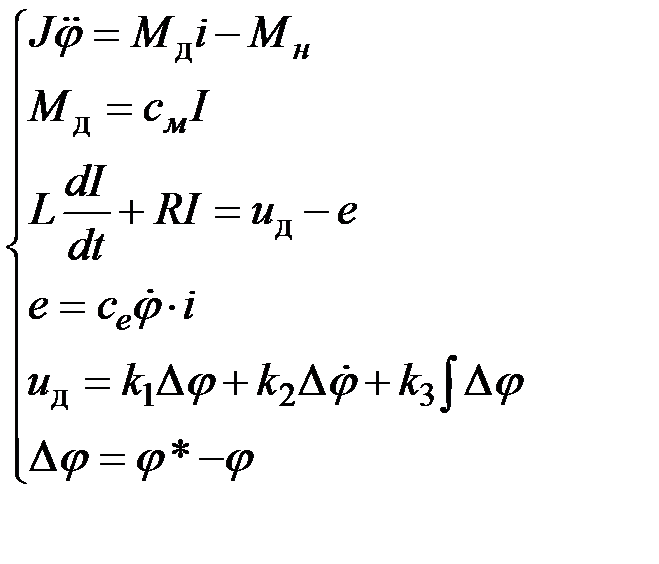
2. Дано описание системы в следующем виде

Уравнение ОУ (объекта управления): .

Найти следующие ПФ: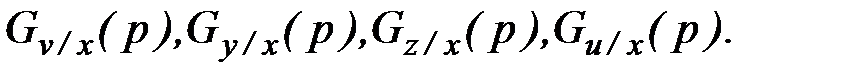

Поиск по сайту: