Управляемость объекта

Если объект полностью управляем, то всегда найдется такое допустимое управление, которое за конечное время обеспечит перевод объекта из любого начального состояния в любое заданное конечное состояние. Оценка управляемости осуществляется на основе критерия Р. Калмана, согласно которому для полной управляемости объекта необходимо и достаточно, чтобы выполнялось условие

.

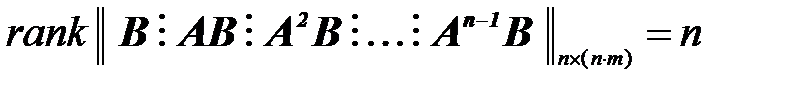Ранг составной матрицы должен равняться порядку системы. Составная матрица имеет n строк и n´m столбцов: первые m столбцов – это столбцы матрицы B, следующие m столбцов - столбцы матрицы AB, затем - матрицы A ² B и т. д.; последние m столбцов, с (n´m-m +1)-го по (n´m)-ый – столбцы матрицы A ^{n -1} B.

Ранг матрицы определяется наивысшим из порядков миноров этой матрицы, отличных от нуля. Так как в рассматриваемой матрице n строк, то проверке подлежат все миноры n –го порядка, которые из нее можно составить (взяв любые n столбцов). Если хотя бы один из таких определителей не будет равен нулю, то критерий Калмана (2.67) выполняется и, следовательно, объект полностью управляем.

В частном случае, когда m = 1 (B = b – столбец размерностью n´ 1), проверка сводится к вычислению единственного определителя .

Пример. Исследуем управляемость объекта в системе двигатель – редуктор–нагрузка.

Математическая модель этой системы была получена ранее:

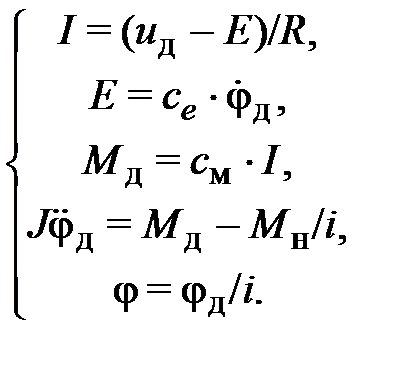
Запишем уравнения динамики в форме Коши:

Входом системы является напряжение , подаваемое на двигатель, выходом – угловое положение вала нагрузки Величина является возмущением (момент нагрузки).

Запишем уравнения модели в матричном и стандартном видах

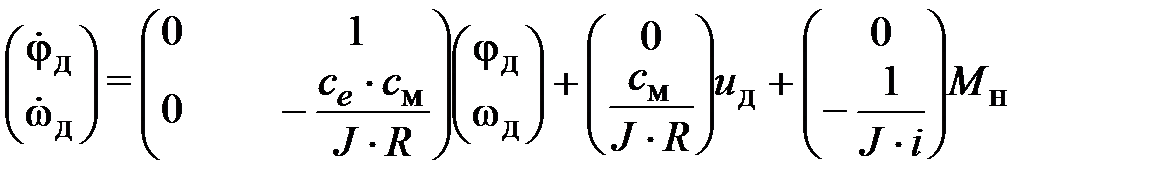
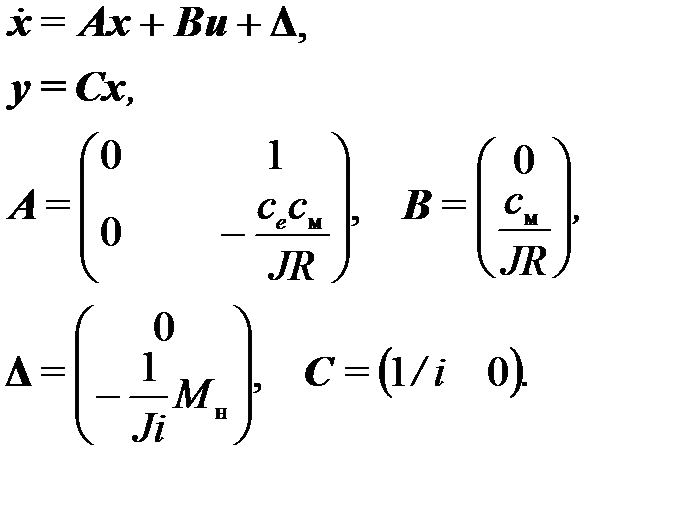
где

Найдем определитель блочной матрицы . В нашем случае n = 2, m = 1 (две переменные состояния и один управляющий сигнал).

.

Блочная матрица принимает вид :

.

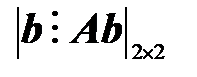Ее определитель не равен нулю и, значит, ранг этой матрицы равен 2. Критерий Калмана выполняется, рассматриваемая система является полностью управляемой. За счет выбора управляющего сигнала можно обеспечить любые значения угловой скорости w_д = и углового ускорения e_д = вала двигателя.

Отметим, что в некоторых случаях проверка критерия Калмана упрощается – в случае, когда матрица А объекта имеет каноническую диагональную форму (2.68) или каноническую жорданову форму (2.69), а также при известном ранге матрицы B.

Если матрица А объекта имеетканоническую диагональную форму (2.68), то согласно критерию Е. Гильберта для полной управляемости такого объекта необходимо и достаточно, чтобы матрица В не содержала нулевых строк.

где l₁ ¹ l₂ ¹ … ¹ l_n.

Если матрица A объекта имеет каноническую жорданову форму (2.69), то для полной управляемости такого объекта необходимо и достаточно, чтобы последняя строка матрицы B была ненулевой.

Наконец, если модель объекта может быть представлена в нормальной форме, когда в качестве переменных состояния выбираются сама управляемая величина y и n –1 ее производных, то такой объект полностью управляем.

В этом случае

На практике для исследования управляемости ранги обычно не считают, а используют компьютерные программы. В частности, в MATLAB функция ctrb собирает аргумент B, AB, A ² B, …, а функция rank считает определитель: rank (ctrb (A,B)).

Управляемость по выходу

Критерий полной управляемости по выходу в общем случае имеет вид

где q – число выходных переменных объекта (или число строк матрицы C).

Для примера с двигателем имеем:

y = j Þ q = 1.

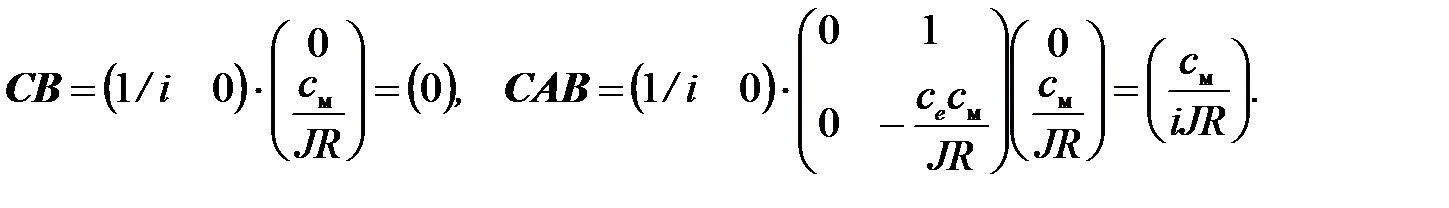
Определитель не равен нулю, ранг равен единице. Критерий полной управляемости по выходу выполнен. Следовательно, за счет выбора управляющего сигнала можно обеспечить любые значения выхода (углового положения нагрузки).

Поиск по сайту: