Критерий В.М. Попова

Задачу исследования абсолютной устойчивости системы с одной однозначной нелинейностью можно решить с помощью частотного критерия Попова. При этом используются приемы, аналогичные частотным способам исследования устойчивости линейных систем.

Если в системе автоматического регулирования имеется лишь одна однозначная нелинейность z = Ф(e), то можно объединить вместе все остальные (линейные) звенья системы и представить ее, как показано на рис. 5.17.

Пусть нелинейность z = Ф(e) имеет любое очертание, не выходящее за пределы заданного угла arctg k (рис. 5.18), т. е. при любом e > 0 Ф(e) < ke, а при e > 0 Ф(e) > ke.

Рис. 5.18. Вид рассматриваемой нелинейности

Пусть многочлен Q (p) (характеристический полином линейной части системы) имеет все корни с отрицательными вещественными частями. Тогда, согласно теореме В.М. Попова, для доказательства устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, при котором для всех w ³ 0 выполняется неравенство

где G(i w ) – амплитудно-фазовая частотная характеристика линейной части системы.

При наличии одного нулевого полюса G (p) требуется еще, чтобы Im G (i w) ® –¥ при w ® 0, а при двух нулевых полюсах, чтобы Re G (i w) ® –¥ при w ® 0, a Im G (i w) < 0 при малых w. Теорема справедлива также и при наличии в знаменателе передаточной функции линейной части не более двух чисто мнимых корней, но при этом требуются некоторые другие простые добавочные условия, называемые условиями предельной устойчивости.

Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики G *(i w), которая определяется следующим образом:

Re G *(i w) = Re G (i w), Im G *(i w) = w× Im G (i w)

или U *(w) = U (w), V *(w) = w V (w).

Тогда

(1 + i w h) G (i w) = (1 + i w h)(U + iV) = U – w hV + i (V + w hU) Þ

Re {(1+ i w h) G (i w)} + 1/ k = U * –hV * + 1/ k.

Условие теоремы В.М. Попова принимает вид

Очевидно, что равенство 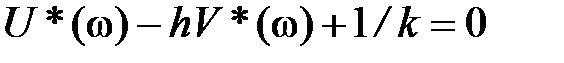представляет собой уравнение прямой на плоскости G *(i w): откуда для условий выполнения теоремы Попова следует:

, h > 0

, h < 0.

Прямая делит всю плоскость U * V * на две полуплоскости. Условие Попова выполняется в одной из полуплоскостей, той где находится точка (0, 0). Следовательно, именно в эту полуплоскость и должна полностью попадать кривая G *(i w). Отсюда следует графическая интерпретация теоремы В.М. Попова: для устойчивости нелинейной системы достаточно подобрать на плоскости G *(i w) прямую, которая бы проходила через точку
(–1/ k, i 0) так, чтобы вся кривая G *(i w) лежала справа от этой прямой (рис. 5.19, а). На рис. 5.19, б показаны случаи, когда теорема не выполняется, т. е. нелинейная система не имеет абсолютной устойчивости.

Рис. 5.19. Графическая интерпретация критерия Попова:

а – устойчивость; б – неустойчивость

Описанный частотный критерий устойчивости В.М. Попова для систем с одной однозначной нелинейностью в его графической форме может быть применен при любой сложности линейной части системы и численно заданных коэффициентах уравнений. Более того, он может быть применен в случае, когда не заданы уравнения, но известна экспериментально снятая амплитудно-фазовая частотная характеристика G (i w) линейной части.

Чтобы исследовать устойчивость системы, нужно перестроить снятую амплитудно-фазовую характеристику G (i w) линейной части в модифицированную характеристику G *(i w). Очертание нелинейности может быть неизвестным. Необходимо знать лишь, в пределах какого угла она расположена. Для конкретно заданных форм нелинейности область устойчивости, вообще говоря, будет несколько шире, но данным методом это определено быть не может.

Пример. Исследование устойчивости нелинейной следящей системы методом Попова.

Предполагается, что ДОС имеет нелинейность типа «зона нечувствительности», (рис. 5.20, а), а усилитель – нелинейность типа «ограничение» (рис. 5.20, б).

Рис. 5.20 – Вид нелинейности системы:

а, б – нелинейности и усилителя; в – нелинейность системы

Предполагается, что в системе реализуется пропорционально-дифференциальный закон управления U = (1 + a p) u, где u – напряжение на выходе усилителя, U – напряжение в якорной цепи двигателя.

Математическая модель объекта управления имеет вид:

Структурная схема системы изображена на рис. 5.21.

Рис. 5.21. Структурная схема системы

Характеристика нелинейности:

Передаточная функция линейной части системы имеет нулевой полюс p = 0 и отрицательный полюс p = –1/ Т.

Условия критерия Попова для нелинейности выполняются при k = k _y, т. к. нелинейность не выходит за пределы допустимого сектора: | u | = |Ф(e)| < k _y| e |. Проверяем частотное условие.

Так как данное неравенство должно иметь место при любом
0£ w <¥, то:

Величину h, удовлетворяющую этим условиям, можно подобрать при любых k_y > 0, a >0: h > max { T – a – c _e/ k _y; – Tc _e / k _ya}. В этом случае условия критерия Попова выполнены и отрезок [– e ₁, e ₁] является поточечно устойчивым в целом, т. е. при любых начальных отклонениях установится режим, в котором e (t) = e _¥, | e _¥| £ e ₁. Значит и j(t) ® j_¥ = – e _¥. Иначе говоря, управляющее воздействие обеспечивает стабилизацию в окрестностях j = j* с точностью до | e ₁|. За погрешность «несет ответственность» зона нечувствительности датчика.

Тот же результат можно получить геометрически. Годограф

целиком лежит в третьем квадранте и легко провести прямую линию, оставляющую его справа (рис. 5.22).

Рис. 5.22. Структурная схема системы

Оказывается, что сформулированный критерий Попова можно применять не только в случае однозначной стационарной характеристики Ф(e). Условие Re [(1+ ih w) G (i w)]+1/ k > 0 остается достаточным при сформулированных выше требованиях, но:

· для неоднозначной характеристики с отрицательным гистерезисом при 0 £ h <¥;

· для неоднозначной характеристики с положительным гистерезисом при –¥ < h <0;

· для нестационарной однозначной и неоднозначной характеристики при h = 0.

Рис. 5.23. Нестационарная однозначная нелинейность

Поиск по сайту: