 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частотные характеристики импульсных систем
Для дискретных систем, так же как и для непрерывных, вводится частотная передаточная функция

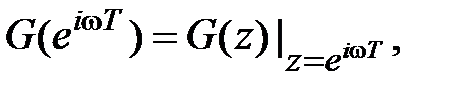
где G (z) – дискретная передаточная функция системы.
Частотная передаточная функция импульсной системы зависит от частоты w, является периодической функцией частоты (а не времени!); период этой функции w0 = 2p/ T. Частотная передаточная функция позволяет определить реакцию импульсной системы на гармоническую последовательность на входе.
Если на входе импульсной системы (импульсного фильтра) с передаточной функцией G (z) действует гармонический сигнал
x (n) = a× sin(n w T), то сигнал y (n) на выходе системы также является гармоническим. Выходная последовательность изменяется с той же частотой, что и входная, и определяется формулой
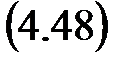 y (n) = a | G (ei w T)|sin(n w T + arg(G (ei w T)).
y (n) = a | G (ei w T)|sin(n w T + arg(G (ei w T)).
Амплитуду и фазу последовательности на выходе можно найти по комплексному выражению G (ei w T). Отношение амплитуд выходного и входного сигналов равно модулю, а разность их фаз – аргументу этого выражения.
Пример. Непрерывная часть импульсного фильтра является апериодическим звеном с передаточной функцией G 0(р) = k /(T0p + 1). Импульсный элемент генерирует короткие прямоугольные импульсы продолжительностью t и = g T. Определим частотные характеристики фильтра.

| f |
| t |
| t |
Передаточная функция приведенной непрерывной части системы, включая экстраполятор

Теперь вычисляем передаточную функцию импульсной системы, как Z -преобразование G п(р)

Передаточная функция e -g pT соответствует звену запаздывания. Из теории известно, что при наличии в системе звена запаздывания
e -t p с величиной запаздывания t меньше периода квантования Т (а в нашем случае t = g T < T) Z -преобразование вычисляется по формуле


Следовательно,
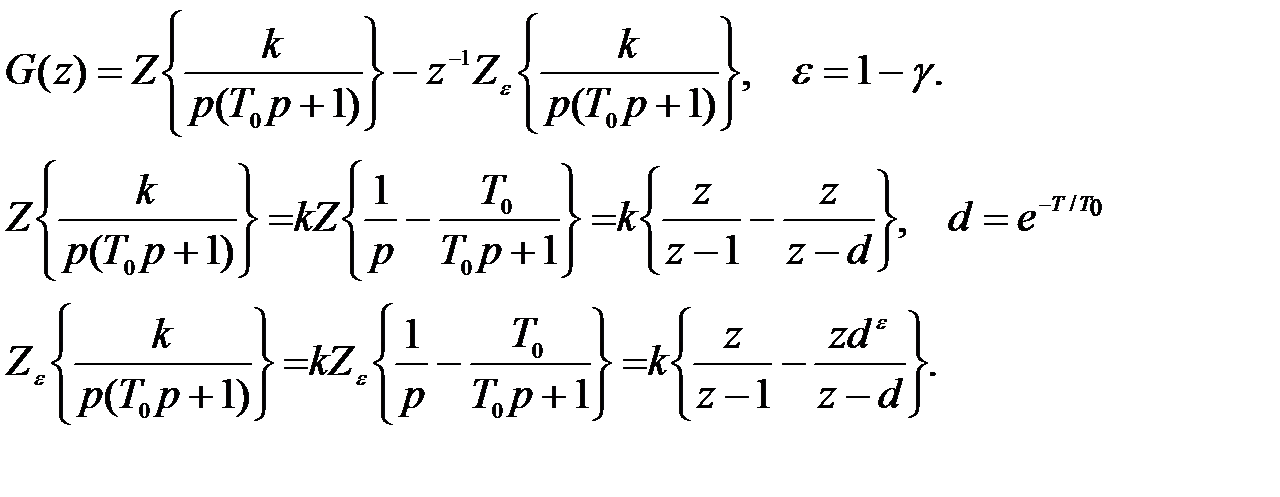


Итак, если на входе действует последовательность
x (n) = a sin(n w T), то на выходе получим
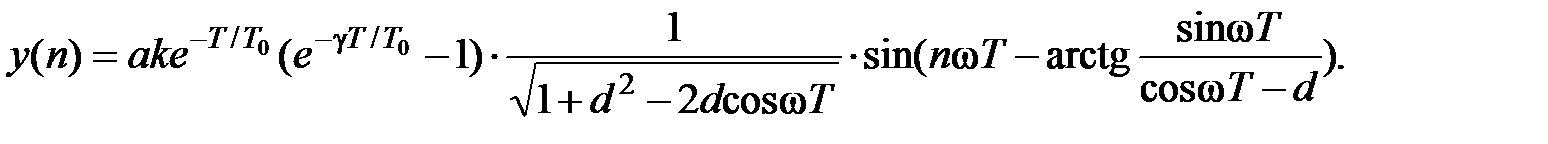
Поиск по сайту: