Свойства ПИД-регулятора

В промышленных системах управления широко используются трехканальные ПИД-регуляторы благодаря простой структуре и реализации, легкости настройки (не требующей глубокого знания теории автоматического управления), возможности применения с широким классом объектов управления. Выход ПИД-регулятора
(рис. 3.14) представляет собой сумму трех компонентов:

1. Усиленного в K _праз сигнала ошибки (рассогласования e (t) между уставкой y *(t) и реальным значением выхода y (t)) – пропорциональный канал.

2. Усиленного в K _и раз интеграла от сигнала ошибки – интегральный канал.

3. Усиленной в K _д производной по времени от сигнала ошибки – дифференциальный канал.

Рис. 3.14. Структурная схема ПИД-регулятора

ПИД-регулятор включается между входом объекта управления и сигналом ошибки , где y * – уставка выходного сигнала. Уравнение выхода ПИД-регулятора , как зависимость от сигнала ошибки , записывается в виде

Поскольку ПИД-регулятор представляет собой линейное звено, то для него можно записать передаточную функцию

Как видно из (3.23) и (3.24), поведение ПИД-регулятора зависит от трех чисел: коэффициентов K _п, K _и, K _д (или Т _и, Т _д – лишь три параметра являются независимыми, а два оставшихся определяются с помощью уравнений связи). Таким образом, задача настройки ПИД-регулятора состоит в подборе таких коэффициентов K _п, K _и, K _д, чтобы добиться устойчивости системы с замкнутой обратной связью и обеспечить заданные характеристики регулирования. В зависимости от знаков и величины параметров К _п, К _и и К _д на основе ПИД-регулятора могут быть построены различные виды регуляторов (рис. 3.15).

Например, при неотрицательных К _п, К _и и К _д, кроме тривиального пропорционального управления (К _и = К _д = 0), имеем:

· изодромный ПИ-регулятор (К _д = 0, рис. 3.15, а);

· ПД-регулятор (К _и=0, рис. 3.15, б);

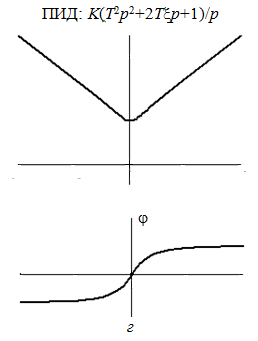
· регулятор с двумя форсирующими звеньями (К ²_п>4 К _и К _д, рис. 3.15, в);

· регулятор с форсирующим звеном 2-го порядка (К ²_п<4 К _и К _д, рис. 3.15, г).

Пропорциональный канал управления ПИД-регулятора является базовым и обеспечивает стабилизацию системы, подавление возмущений и компенсацию неопределенность модели. Теоретически, пропорциональный регулятор может управлять объектами с моделями первого порядка без возмущений. При наличии возмущений или неточностей модели объекта управления пропорциональный регулятор обычно также позволяет решать базовые задачи управления, но при этом приходится применять большие значения коэффициента К _п. На практике это следует делать с осторожностью, поскольку большое значение К _п может привести к усилению шума датчика обратной связи и потери устойчивости системы.

Интегральный канал используется для достижения высокой точности управления и позволяет уменьшить пропорциональную составляющую регулятора, сохранив при этом точность. Интегральный канал необходим при воздействии аддитивных возмущений на объект управления. Однако при добавлении интегральной составляющей может уменьшиться запас устойчивости системы и появиться перерегулирование.

Дифференциальная составляющая позволяет управлять производной выхода объекта управления. Если объект управления представляет собой систему второго порядка (в частном случае, является двойным интегратором), то дифференциальная составляющая обычно необходима. Поскольку реализация дифференциатора представляет собой фильтр высоких частот, то ее применение всегда увеличивает шум в управляющих воздействиях. Дифференциатор значительно усиливает шум датчика обратной связи, который обычно имеет высокочастотный спектр. Однако наличие этой составляющей благоприятно сказывается на увеличении запаса устойчивости системы.

С позиций частотного анализа влияние различных составляющих ПИД-регулятора на ЛАЧХ регулятора L _р(w) проявляется в следующем.

· Пропорциональная составляющая К _п задает минимально возможный уровень усиления сигнала ошибки e (t), что доказывает АЧХ ПИД-регулятора

Увеличение модуля коэффициента пропорционального усиления К _п поднимает среднечастотную часть амплитудной характеристики L _р(w), что влечет аналогичный подъем в этом же частотном диапазоне амплитудной характеристики разомкнутой системы L _раз(w) и сдвиг вправо ее частоты среза. Если не нарушаются запасы устойчивости, то такой прием позволяет повысить быстродействие замкнутой системы, расширяет полосу пропускания, снижает установившуюся ошибку. Отметим, что при этом проявляются и побочные отрицательные эффекты в виде некоторого роста перерегулирования и колебательности из-за приближения к границе устойчивости.

· Включение в состав регулятора интегральной составляющей К _и/ р увеличивает порядок астатизма разомкнутого контура на единицу. При этом для статического объекта управления в устойчивой замкнутой системе ошибка стабилизации постоянного входного воздействия с течением времени придет к нулю. Точнее канал интегрального управления объектом с порядком астатизма n за счет интегральной составляющей обеспечивает нулевую установившуюся невязку слежения за полиномиальной уставкой n -ой степени. Увеличение коэффициента интегрального усиления К _и поднимает низкочастотную часть амплитудной характеристики L _р(w) и разомкнутой системы в целом_.

· Дифференциальная составляющая регулятора К _д р предназначена для подъема фазовой характеристики разомкнутого контура в средне- и высокочастотном диапазонах с целью устранения неустойчивости замкнутой системы либо для увеличения запаса устойчивости по фазе. Увеличение коэффициента К _д поднимает высокочастотную часть амплитудной характеристики L _р(w). В результате увеличиваются запасы устойчивости, уменьшается колебательность и форсируется переходный процесс замкнутой системы.

Следует заметить, что теоретически ПИД-регулятор может быть использован только для объектов управления, описываемых моделями не более второго порядка. Однако, поскольку на практике в большинстве случаев встречаются именно такие объекты, ПИД-регуляторы применяются почти повсеместно.

Возможны различные варианты определения коэффициентов K _п, K _и, K _д:

1. Ручная настройка ПИД-регулятора, при которой параметры K _п, K _и, K _д выбираются на основе эмпирических правил по результатам моделирования и испытания системы управления.

2. Вычисление коэффициентов ПИД-регулятора на основе желаемого вида передаточной функции и метода неопределенных коэффициентов.

3. Графо-аналитический метод, основанный на использовании логарифмических частотных характеристик.

4. Оптимизационный метод с использованием компьютерных процедур.

Поиск по сайту: