Передаточная функция импульсного звена

Рассмотрим разностное уравнение в общем виде, когда правая часть зависит от значений входного сигнала не только в данный, но и в предшествующие моменты времени:

a ₀ y (n+m) + a ₁ y (n+m– 1) + …+ a_my (n) = b ₀ х (n+k) + …+ b_kх (n).

Перейдя в (4.24) с помощью Z -преобразования к операторной форме, с учетом нулевых начальных условий получим

Изображение искомой решетчатой функции равно

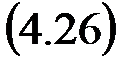
Здесь введена дискретная передаточная функция G (z), которая, как и в случае непрерывных функций, является отношением двух изображений (выходной и входной величин) при нулевых начальных условиях

Дискретная передаточная функция играет такую же роль в импульсных и цифровых системах, как и обычная передаточная функция в непрерывных системах. В частности, ПФ позволяет определить реакцию звена на заданное входное воздействие.

Пример. На звено с передаточной функцией действует входной сигнал x (n) = 1(n). Определим выходной сигнал y (n).

Z-преобразование выходного сигнала имеет вид

1) Разложение в ряд Лорана

Так как по определению Z –преобразования

т. е. y (n) – коэффициенты функции Y (z) при степенях z ^{– n}, то коэффициенты y (n) искомой решетчатой функции можно получить разложением Y (z) в ряд Лорана, разделив числитель функции Y (z) на ее знаменатель.

z² z²–1,5z+0,5

z²–1,5z+0,5 1+1,5/z+1,75/z²+1,875/z³…

1,5z–0,5

1,5z–2,25+0,75/z

1,75–0,75/z

1,75–2,625/z+0,875/z²

1,875/z–0,875/z²

1,875/z–2,8125/z²+0,9375/z³

………………………………………

Таким образом

Следовательно, y (0) = 1; y (1) = 1,5; y (2) = 1,75; … y (n) = 2 – 2^{- n} .

2) Использование таблиц Z -преобразования

Раскладываем Y (z) на простые дроби, для которых имеются табличные выражения обратного Z -преобразования.

3) Правило свертки

Если Y (z) = G (z)∙ X (z), где G (z) = Z { g (n)}, X (z) = Z { x (n)}, то

В нашем случае x (n) = 1(n), g (n) = Z ^-1{ G (z)} = Z ^-1{ z /(z –0,5)} = (1/2) ⁿ (из таблицы).

Тогда

Поиск по сайту: