Особые траектории

Различают три основных типа особых траекторий:

1. Особые точки (состояние равновесия). Типы особых точек рассмотрены выше.

2. Изолированные замкнутые траектории. Изолированность замкнутой траектории означает, что в достаточно малой ее окрестности нет других замкнутых траекторий. Изолированные замкнутые траектории называются предельными циклами. Предельным циклам на фазовой плоскости соответствуют периодические движения системы.

Предельный цикл называется устойчивым, если существует такая окрестность этого цикла, что все фазовые траектории, начинающиеся в этой окрестности, асимптотически при приближаются к предельному циклу (рис. 5.13, а).

Устойчивым предельным циклам в системе автоматического управления соответствуют автоколебания. Характерная черта автоколебаний – локальная независимость их параметров от начальных условий.

а б

Рис. 5.13. Фазовый портрет маятника:

а – устойчивый предельный цикл; б – неустойчивый

Если в любой, сколь угодно малой окрестности предельного цикла существует хотя бы одна фазовая траектория, не приближающаяся к предельному циклу при , то предельный цикл называется неустойчивым (рис. 5.13, б).

3. Сепаратрисы разделяют фазовую плоскость на области с фазовыми траекториями различных типов. В окрестности особой точки типа «седло» сепаратрисы являются асимптотами.

Обычно на фазовой плоскости особых траекторий (т. е. точек равновесия, предельных циклов и сепаратрис) имеется конечное число. Определив их, находят все качественные особенности фазовых траекторий на плоскости, а по ним - все виды и особенности процессов в нелинейных системах.

Пример. Фазовый портрет релейной системы (рис. 5.14).

Рис. 5.14. Релейная система

В случае нелинейного элемента типа “реле с зоной нечувствительности” можно сразу найти положения равновесия: z = 0 как вход интегратора k/p в равновесном состоянии: ½ x ½ £ d; ½ y ½£ d. Имеет место отрезок равновесия.

Для построения фазового портрета запишем дифференциальные уравнения системы в форме Коши:

Если учесть, что функция F (x ₁) кусочно-линейная, то переменные можно разделить и проинтегрировать уравнение на различных интервалах x ₁

где С – постоянная, определяемая начальными условиями.

Для различных интервалов изменения x ₁получим следующие уравнения для фазовых траекторий:

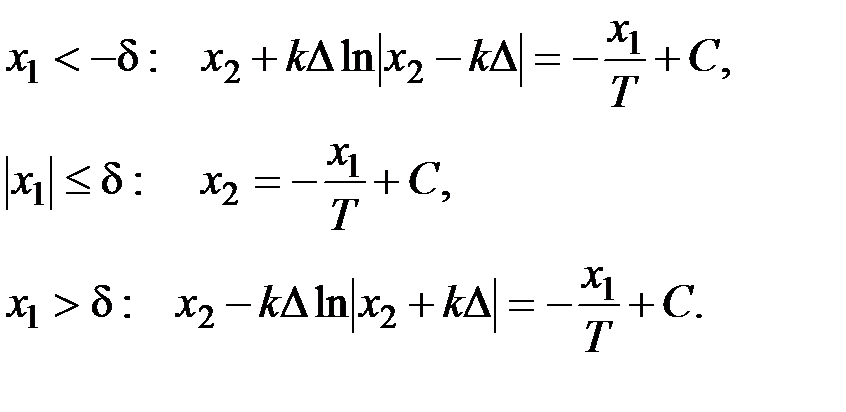
На рис. 5.15 показан фазовый портрет релейной системы “с зоной нечувствительности”. Линиям x ₁= ±d(так называемым линиям переключения реле)соответствуют границы трех “листов” (частей) фазовой плоскости. Движения системы завершаются на отрезке равновесия.

Если модель системы содержит НЭ с кусочно-постоянной (или кусочно-линейной) характеристикой, то процесс может быть разбит на ряд интервалов так, что в пределах каждого интервала движение описывается линейными дифференциальными уравнениями.

Рис. 5.15. Фазовый портрет системы с НЭ типа
“реле с зоной нечувствительности”

На фазовой плоскости каждому линейному участку такой характеристики нелинейного элемента соответствует отдельная область или лист, в пределах которого правые части дифференциальных уравнений линейны, а фазовые траектории составлены из дуг траекторий линейных систем. Излому или разрыву таких статических характеристик нелинейных элементов соответствует граница листа фазовой плоскости (линия переключения).

Если нелинейный элемент имеет характеристику типа реле с гистерезисом, то система не может иметь положений равновесия, так как всегда z ¹ 0. Фазовая плоскость состоит из двух листов. Границами листов являются в верхней полуплоскости прямая x ₁= d, а в нижней – прямая x ₁= –d. Фазовый портрет показан на рис. 5.16. Выделяется устойчивый предельный цикл; система функционирует в автоколебательном режиме.

Анализ показывает, что фазовые траектории, начинаясь из произвольной точки фазовой плоскости, сходятся к некоторой замкнутой кривой, т. е. образуют сходящиеся спирали. На фазовой плоскости есть предельный цикл, следовательно, в системе есть автоколебания.

Рис. 5.16. Фазовый портрет системы с НЭ типа “реле с гистерезисом”

Если начальные условия таковы, что изображающая точка находится внутри предельного цикла, то процесс в системе будет иметь вид, представленный на рис. 5.17, а. Если начальные условия на фазовой плоскости лежат вне предельного цикла, то процесс будет иметь вид, представленный на рис. 5.17, б. Автоколебания происходят около петли гистерезиса с амплитудой, несколько превышающей величину b.

а б

Рис. 5.17. Автоколебания

Поиск по сайту: