Скользящие процессы в релейных системах

Рассмотрим систему автоматического управления с нелинейным элементом типа «идеальное реле» (рис. 5.18). Структурная схема исследуемой системы показана на рис. 5.19. Построим и исследуем фазовые траектории этой системы.

Рис. 5.18. Характеристика «идеального реле»

Рис. 5.19. Структурная схема исследуемой системы с «идеальным реле»

По заданной структурной схеме составим математическую модель в виде системы дифференциальных уравнений

Преобразуем математическую модель исследуемой системы с учетом свойств релейной характеристики (нечетная функция)

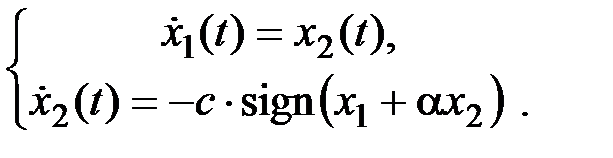
Движение системы происходит только за счет ненулевых начальных условий. Переменные состояния имеют следующий смысл: х ₁ – выход, х ₂ – скорость изменения выхода. Получим дифференциальное уравнение фазовых траекторий системы

.

Линия переключения реле на фазовой плоскости задается уравнением , .

Справа от линии переключения (область I) будет выполняться неравенство , слева - неравенство (область II). Получим уравнения фазовых траекторий в каждой из этих областей.

Область I: , dx ₂/ dx ₁ = – c/x ₂ – это дифференциальное уравнение с разделяющимися переменными:

, , .

Уравнение фазовых траекторий системы в области I – это уравнение парабол, вершины которых находятся на оси x ₁ фазовой плоскости, а ветви парабол направлены влево. Параболы изображены на рис. 5.20 справа от линии переключения.

Рис. 5.20. Фазовые траектории в областях I и II

Направление движения изображающей точки по этим фазовым траекториям: в верхней полуплоскости – движение слева направо, в нижней полуплоскости – справа налево.

Область II: , dx ₂/ dx ₁ = c/x ₂, – это дифференциальное уравнение фазовых траекторий исследуемой системы слева от линии переключения – уравнение парабол, вершины которых находятся на оси x ₁, а ветви парабол направлены вправо. Направление движения изображающей точки: в верхней полуплоскости – справа налево, в нижней полуплоскости – слева направо.

«Сшивая» оба листа по линии переключения, получим фазовый портрет исследуемой системы (рис. 5.21).

Рис. 5.21. Фазовый портрет системы

Пусть начальные условия таковы, что изображающая точка на фазовой плоскости занимает положение М₀ в области I. Здесь и дальнейшее движение изображающей точки происходит по фазовой траектории М₀М₁М₂. В точке М₂ происходит переключение реле (изображающая точка достигла линии переключения). Далее изображающая точка перемещается по фазовой траектории М₂М₃. В точке М₃ изображающая точка достигает линии переключения внутри отрезка АВ – отрезка скольжения.

На линии скольжения происходит следующее. Как только фазовая траектория пересечет линию переключения (из области II в область I), вступит в свои права фазовая траектория из области I, которая вернет процесс на линию переключения внутри отрезка скольжения. Но тут попадаем на фазовую траекторию из области II и т. д. В результате изображающая точка будет «скользить» по линии переключения к началу координат. Это соответствует переключениям релейного элемента с большой частотой. Теоретически частота колебаний бесконечна, а их амплитуда равна нулю. Следовательно, теоретически изображающая точка скользит по линии переключения к началу координат – равновесному состоянию. Фазовой траектории М₀М₁М₂М₃ соответствует процесс во времени, показанный на рис. 5.22, где отмечены те же характерные точки.

Рис. 5.22. Траектория движения

Из полученных формул и фазового портрета исследуемой системы можно сделать следующие выводы.

1. Фазовая плоскость исследуемой системы разбивается на две области, границей которых является прямая – линия переключения релейного элемента системы.

2. На линии переключения можно выделить три характерных участка, разграниченных точками А и В – точками касания фазовых траекторий (парабол) линии переключения. За пределами отрезка АВ фазовая траектория по одну сторону линии переключения после перехода через нее является продолжением траектории по другую сторону линии переключения. Внутри отрезка АВ фазовые траектории подходят к линии переключения с двух сторон, встречаясь на нем.

3. Попав на отрезок АВ, изображающая точка уже не сможет сойти с него, но и не сможет остаться на нем. Скорость движения на АВ не определена, но специальные исследования показывают, что она конечна. Изображающая точка будет скользить по отрезку к началу координат – точке равновесия, похожей на устойчивый узел. Отрезок АВ называют отрезком скольжения.

Уравнение движения системы вдоль линии переключения или . Решение этого уравнения будет , где значения t = 0 (начальное значение времени движения системы по линии переключения) и x ₁(0) = x ₁₀ вычисляются в момент попадания изображающей точки на линию (отрезок) скольжения.

Скользящий процесс происходит по экспоненциальному закону и не зависит от параметров системы, а определяется только коэффициентом обратной связи. Нелинейная система второго порядка на участке скользящего режима вырождается в линейную систему первого порядка.

Найдем положение концов отрезка скользящего процесса A и B на фазовой плоскости. Очевидно, что в этих точках касательные к параболам совпадают с линией переключения. Это условие согласно уравнению можно записать в виде . Тогда из уравнений траекторий получим для точки A условие в виде

; .

Для точки B:

;

4. Отрезок скользящего процесса тем больше, чем больше коэффициент усиления обратной связи.

5.3 Устойчивость нелинейных САУ

Придет ли с течением времени нелинейная система к положению равновесия (или заданного движения) при начальном отклонении от этого состояния? Кажется возможным для нелинейной системы с «гладкой» нелинейностью при малых начальных отклонениях (в пределах линейной зоны) считать и в дальнейшем ее поведение близким к поведению соответствующей линейной системы и использовать известные критерии устойчивости для линеаризованной модели. Однако такой подход неверен. Процесс, начавшийся в «линейной» зоне, даже при выполнении условий устойчивости «в малом», может эту зону покинуть.

При исследовании систем управления по нелинейным математическим моделям следует говорить об устойчивости конкретного движения, а не системы в целом; одни движения нелинейной системы могут быть устойчивыми, а другие ― нет.

Пусть математическая модель системы представлена в форме системы дифференциальных уравнений 1-го порядка (в форме Коши)

где х ― вектор состояния; f ― вектор-функция (нелинейная).

Решения системы (5.23) х* (t, х ₀), при конкретных начальных условиях х ₀ = х (0), следуя Ляпунову[1], называют невозмущенным движением. Выбор движения, принимаемого за невозмущенное, произволен. В частности, если начальным условиям х ₀ соответствует положение равновесия, то оно и будет невозмущенным движением. Всякое другое решение дифференциальных уравнений х (t, х ₀+D х ₀) при иных начальных условиях х ₀+D х ₀ называется возмущенным. Вариация движения – это разность между возмущенным и невозмущенным движениями: D х (t) = х (t, х ₀+D х ₀) – х* (t, х ₀).

Невозмущенное движение называется устойчивым, если для любого e > 0 найдется такое d(e), что из для всех t > T следует: (знак означает норму вектора).

Если в качестве невозмущенного движения принять состояние равновесия системы, то определение устойчивости можно интерпретировать так. Положение равновесия называется устойчивым, если, задав вокруг точки равновесия любую сколь угодно малую область e, можно найти такую область d(e), что помещенная в момент времени t = 0 в любую точку этой области изображающая точка в момент времени t = T войдет в область e и далее из нее не выйдет.

Асимптотическая устойчивость означает, что т. е. возмущенные движения асимптотически стремятся к невозмущенному, в частности, при t ®µ приходят в состояние равновесия.

Устойчивость по Ляпунову ― понятие качественное (теоретическое), поскольку не оговариваются размеры области невозмущенного движения; здесь говорят об устойчивости “в малом”. Устойчивость “в большом” ― понятие количественное (практическое), когда указываются границы области притяжения. В том случае, когда область совпадает со всем пространством состояний, невозмущенное движение будет устойчивым “в целом”.

Линейная система имеет единственное положение равновесия; если оно устойчиво, то устойчиво “в целом”. Разумеется, остается вопрос о том, насколько линейная модель адекватно описывает реакцию системы “в целом”.

Поиск по сайту: