Теорема Лурье

Рассмотрим нелинейную систему с одной однозначной нелинейностью z = Ф(e). Объединив вместе все остальные (линейные) звенья системы, представим ее в следующем виде (рис. 5.17):

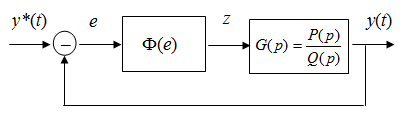
Рис. 5.17. Нелинейная система с обратной связью

Пусть статическая характеристика Ф(е) безынерционного нелинейного элемента удовлетворяет следующим условиям: однозначна и непрерывна; Ф(0) = 0; e ∙Ф(e) > 0, т. е. график характеристики проходит через начало координат и располагается в первом и третьем квадрантах. Для этого практически важного случая А. И. Лурье[2] и В. Н. Постников предложили следующую форму функции Ляпунова (квадратичная форма от е плюс интеграл от нелинейности):

.

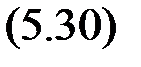
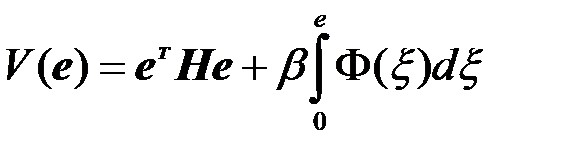Пример.

Пусть линейная часть системы имеет передаточную функцию
G (p) = k /(Tp + 1), а нелинейный элемент удовлетворяет приведенным условиям. При отсутствии воздействия (y* = 0) положению равновесия системы соответствует значение е = 0.

Дифференциальное уравнение системы первого порядка в форме Коши запишется так:

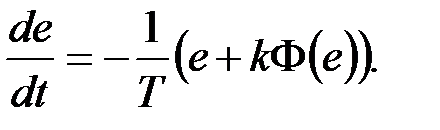
Выберем следующую функцию Ляпунова:

.

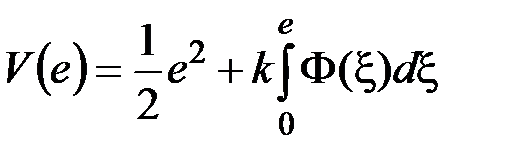Продифференцируем эту функцию по времени, получим:

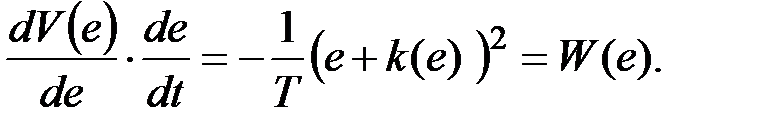
Получили отрицательно-определенную функцию W (е), что позволяет сделать вывод об асимптотической устойчивости положения равновесия. Кроме того, замечаем, что функция 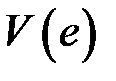определена для всех е и при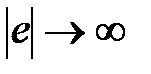 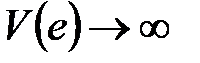. Поэтому положение равновесия асимптотически устойчиво в целом. Наконец, обратим внимание на то, что полученный результат справедлив для целого класса нелинейных функций Ф(е), удовлетворяющих введенным выше ограничениям.

Таким образом, условия устойчивости не зависят от конкретного вида нелинейности и начальных условий. Устойчивость, не зависящая от начальных условий, называется устойчивостью в целом. Устойчивость, не зависящая от конкретного вида нелинейности, называется абсолютной устойчивостью.

Асимптотическую устойчивость в целом для класса нелинейностей называют абсолютной устойчивостью. В рассмотренном примере системы первого порядка положение равновесия абсолютно устойчиво.

Поиск по сайту: