Идентификация объектов

Аналитические методы исследования опираются на математические модели объекта и элементов системы управления. Эти модели получают на основе законов физики, механики, химии и т. д. Такой подход дает положительный результат, если рассматриваемый объект достаточно прост по структуре и хорошо изучен. Если же объект изучен недостаточно или же настолько сложен, что аналитическое описание его математической моделью практически невозможно, прибегают к экспериментальным методам. В этом случае производится статистическая обработка результатов испытаний, по которым «восстанавливается» модель «черного ящика». Может быть использован и экспериментально-аналитический метод, когда априорная модель, полученная аналитическим путем, уточняется в соответствующих экспериментах.

Откуда взять модель системы, если отсутствует описание некоторых ее элементов? Для этого выполняется идентификация системы или ее отдельных подсистем. Различают два типа идентификации: структурную и параметрическую.

При структурной идентификации определяют структуру реального объекта управления в виде математической модели. После того как математическая модель объекта определена, проводят параметрическую идентификацию, заключающуюся в определении числовых параметров математической модели по экспериментальным данным.

Задачу параметрической идентификации можно сформулировать следующим образом. Пусть имеется полностью наблюдаемый и полностью управляемый объект, задаваемый в общем случае уравнениями состояния вида

где B – n -мерный вектор–столбец; C – n -мерный вектор–строка,
А – квадратная матрица размером n × n, причем А, В и С – заранее неизвестны.

Целью идентификации является определение элементов матриц А, В, С. Структурная схема объекта представлена на рис. 2.60.

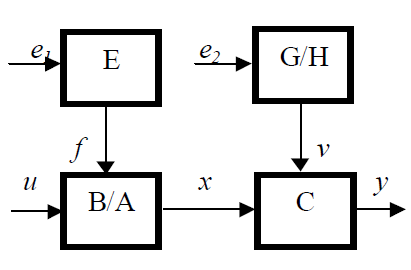
Рис. 2.60. Структурная схема объекта параметрической оптимизации

На схеме приняты следующие обозначения:

u, y – наблюдаемые входной и выходной сигналы;

x – ненаблюдаемая (скрытая) переменная, оцениваемая косвенно по сигналам u и y, получаемым в результате преобразования в системе операторами А, В и H;

е₁, е₂ – ненаблюдаемые помехи (случайные процессы типа белого шума);

f, v – ненаблюдаемые помехи (коррелированные во времени случайные сигналы, в некоторых случаях содержащие детерминированные составляющие);

A, B, C, E, G, H – операторы, вид которых известен, но неизвестны пара­метры.

Основными постановками задач идентификации являются:

– идентификация, или определение характеристик объекта (по значениям u и y определить операторы А, В и C);

– генерация случайных сигналов с заданными характеристиками, или определение характеристик сигналов (по значениям f или v определить оператор E или G, H);

– наблюдение за скрытыми переменными, или определение переменных состояния (по наблюдаемым u и y, известным операторам A, B, C, E, G, H определить x).

Существуют различные методы параметрической оптимизации. В одном случае непосредственно определяются коэффициенты передаточной функции или уравнения объекта. Вторая группа методов используется для определения временных или частотных характеристик объектов, а также характеристик случайных процессов генерируемых объектами. По полученным характеристикам затем определяются передаточная функция или уравнения объекта.

Поиск по сайту: