 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Особенности нелинейных систем
Нелинейные элементы в автоматических системах, как уже сказано, могут быть подразделены на две основные группы:
· естественные – непосредственно присутствующие в системе;
· искусственные – специально вводимые в систему для придания ей нужных свойств.
К первой группе относятся нелинейности типа «насыщение» (рис. 5.1, а), «зона нечувствительности» (рис. 5.1, б), «петля гистерезиса» (рис. 5.1, в). Нелинейность типа «насыщение» характерна для усилителей: при больших значениях входного сигнала выходной сигнал ограничен из-за недостатка мощности источника, питающего усилитель.
| x |
| x |
| x |
| x |
| x |
| x |
| y |
| y |
| y |
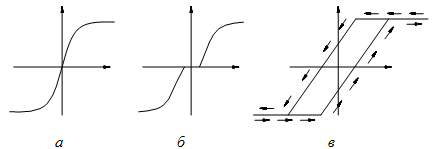
Рис. 5.1 – Типовые нелинейности:
а – насыщение; б – зона нечувствительности; в – гистерезис
«Зона нечувствительности» возникает в усилителях или датчиках, которые не реагируют на малые входные сигналы. Люфт – следствие зазоров в механических передачах.
| y |
| y |
| y |
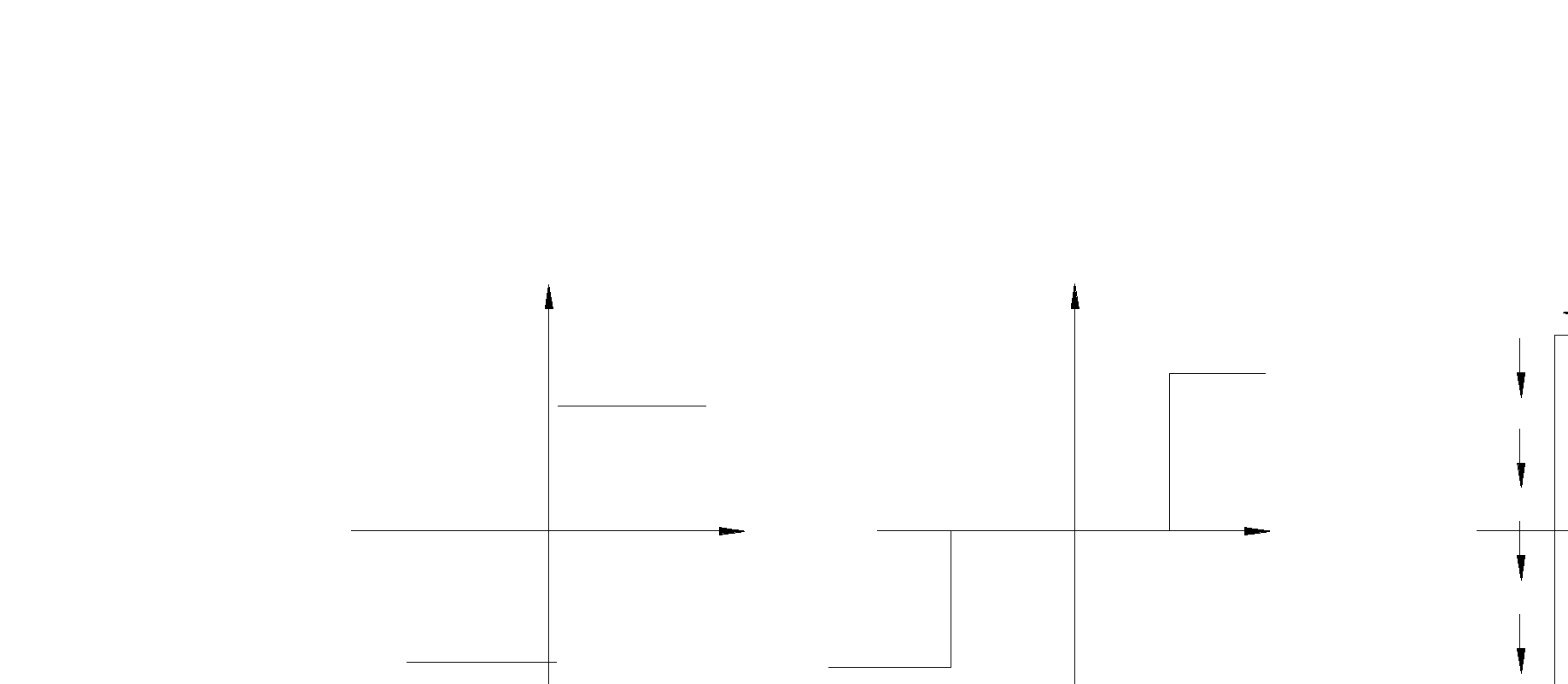
Ко второй группе (искусственные нелинейности) относятся релейные характеристики (рис. 5.2): идеальное реле (рис. 5.2, а), реле с зоной нечувствительности (рис. 5.2, б), реле с гистерезисом (рис. 5.2, в), а также специальные (с кусочно-линейной характеристикой, с криволинейной характеристикой любого очертания и т. д.).
а б в
Рис. 5.2 – Искусственные нелинейности: а – идеальное реле;
б – реле с зоной нечувствительности; в – реле с гистерезисом
Различают статические и динамические нелинейности. Первые представляются в виде нелинейных статических характеристик, т. е. характеризуют нелинейную связь между установившимися значениями выхода и входа, а вторые описываются нелинейными дифференциальными уравнениями, когда выход нелинейно зависит не только от входного сигнала, но и от скорости его изменения или высших производных (пример – вязкое трение).
Исследовать нелинейную систему, как правило, значительно сложнее, чем линейную. Обычно линеаризуют звенья с несущественными нелинейностями и предельно упрощают уравнения существенно нелинейных звеньев.
Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма важных особенностей, отличающих их от линейных систем.
- Не выполняется принцип суперпозиции для математических моделей нелинейных систем автоматического управления. Правила преобразования структурных схем, аналогичных для линейных систем, в общем случае не существуют.
- Так не существуют общие методы решения нелинейных дифференциальных уравнений то, как правило, исследования нелинейных систем носит качественный, приближенный характер.
- Нелинейная система может иметь несколько положений равновесия, в отличие от линейной системы, имеющей единственное положение равновесия. Если линейная система находится не на границе устойчивости, то при любых начальных условиях движение асимптотически затухает к положению равновесия (система устойчива в целом) или расходится (система не устойчива). Реальные (нелинейные) динамические системы могут иметь несколько положений равновесия, например, у математического маятника их бесконечное счетное множество j = k p; k = 0, ±1, ±2,....
- Переходные процессы в нелинейных системах имеют конечную длительность во времени, в отличие от линейных систем, где они теоретически бесконечны.
- Реальные значения переменных, описывающих нелинейные процессы, всегда ограничены энергетическими, материальными, прочностными ресурсами, даже в случае неустойчивости системы. Значения переменных неустойчивой линейной системы неограниченно растут во времени.
- Характер движения в нелинейной системе зависит от начальных условий и уровня воздействий. В реальных системах не выполняется принцип суперпозиции (при сложении воздействий реакция не равна сумме реакций на отдельные воздействия).
Из-за этих особенностей даже вопрос исследования устойчивости системы становится более сложным. Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса имеют значение, в отличие от линейных систем, также и начальные условия. Кроме того, на устойчивость нелинейных систем может существенно влиять величина и вид внешних воздействий. Возможен новый вид установившегося процесса – автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий.
В общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше (рис. 5.3):
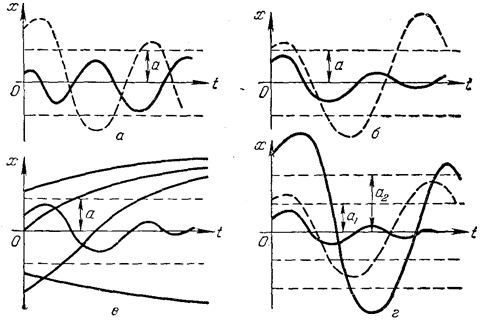
Рис. 5.3. Возможные процессы в нелинейных системах:
а – устойчивые автоколебания; б, в – устойчивость в малом и неустойчивость в большом; г – устойчивые и неустойчивые автоколебания
· область устойчивости равновесного состояния с постоянным значением регулируемой величины;
· область устойчивых автоколебаний;
· область неустойчивости системы;
· области, соответствующие другим, более сложным вариантам поведения.
Если процессы в системе имеют вид, указанный на рис. 5.3, а, то равновесное состояние (х = 0) неустойчиво. В том случае, когда оба указанных на рис. 5.3, а колебания в переходных процессах стремятся к одной и той же амплитуде и к одной и той же частоте, система будет обладать устойчивыми автоколебаниями с амплитудой а.
На рис. 5.3, б, в показаны случаи, когда равновесное состояние
(х = 0) системы устойчиво «в малом» (при начальных условиях, не выводящих отклонения в переходном процессе за величину а), и неустойчиво «в большом» (при начальных условиях, выводящих отклонение в переходном процессе за пределы величины а).
На рис. 5.3, г показан случай трех возможных установившихся состояний: равновесное состояние (х = 0); колебания с постоянной амплитудой a 1; колебания с постоянной амплитудой a 2. Отметим, что колебания с амплитудой a 1 неустойчивы. Система устойчива «в малом» по отношению к равновесному состоянию х = 0, а «в большом» наблюдаются устойчивые автоколебания с амплитудой a 2.
Для иллюстрации особенностей нелинейной системы рассмотрим пример.
Пример. Автоколебания в релейной системе автоматического регулирования скорости вращения двигателя.
Считаем, что используемый датчик скорости имеет релейную характеристику с гистерезисом (рис. 5.4).
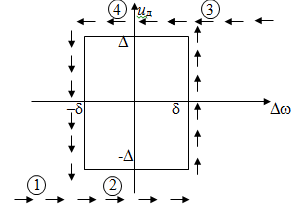
Рис. 5.4. Датчик с релейной характеристикой с гистерезисом
Составим математическую модель системы и будем использовать для решения «метод сшивания траекторий» или «метод припасовывания».
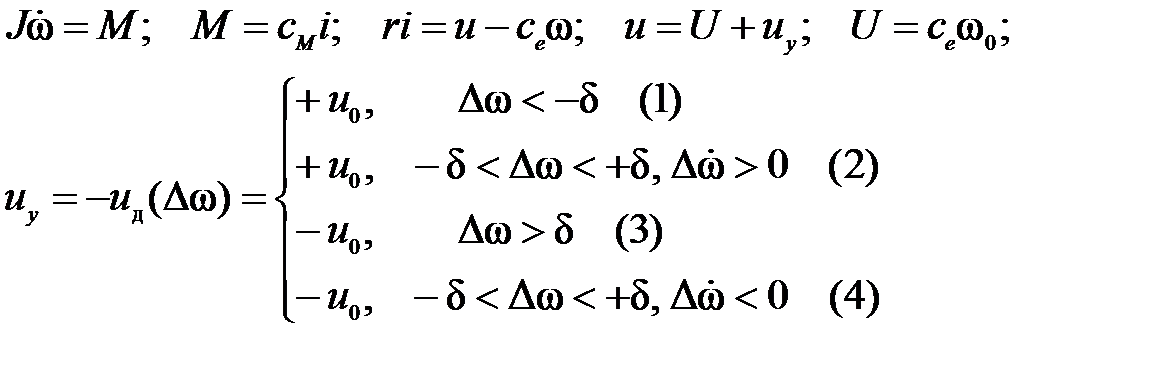
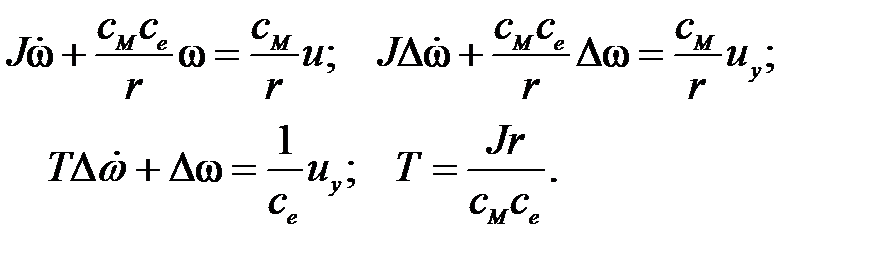
Предположим для определенности, что в исходном состоянии
(t = 0) отклонение скорости w вращения двигателя от требуемого значения w0 составляет Dw(0) = D >d.
1-ый этап: Dw > d, u = – u 0 (участок 3, 4)
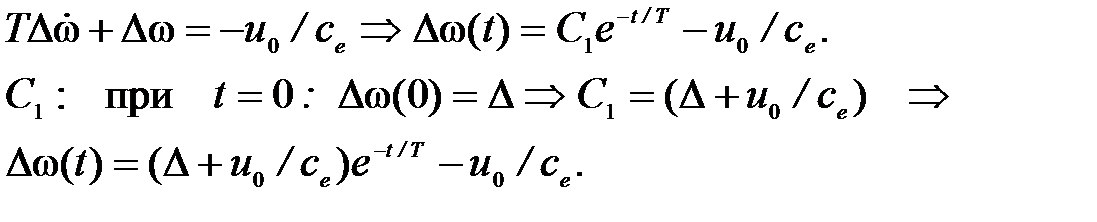
Переключение на другую траекторию происходит при t = t 1, когда Dw(t 1) = –d.
Момент переключения определяем следующим образом:
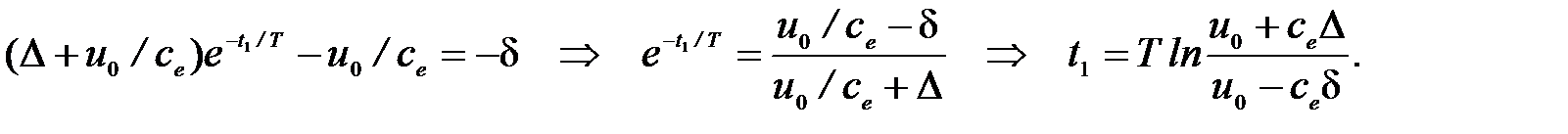
2-ой этап: –d < Dw < d, u = + u 0 (участок 1, 2)

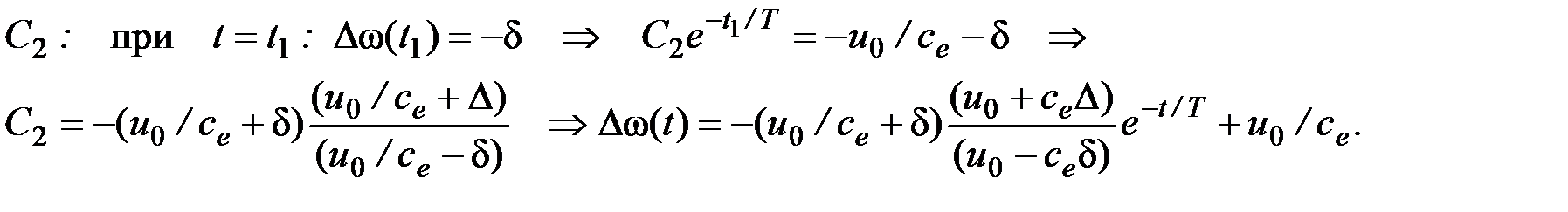 Переключение происходит при t = t 2, когда Dw(t 2) = d.
Переключение происходит при t = t 2, когда Dw(t 2) = d.
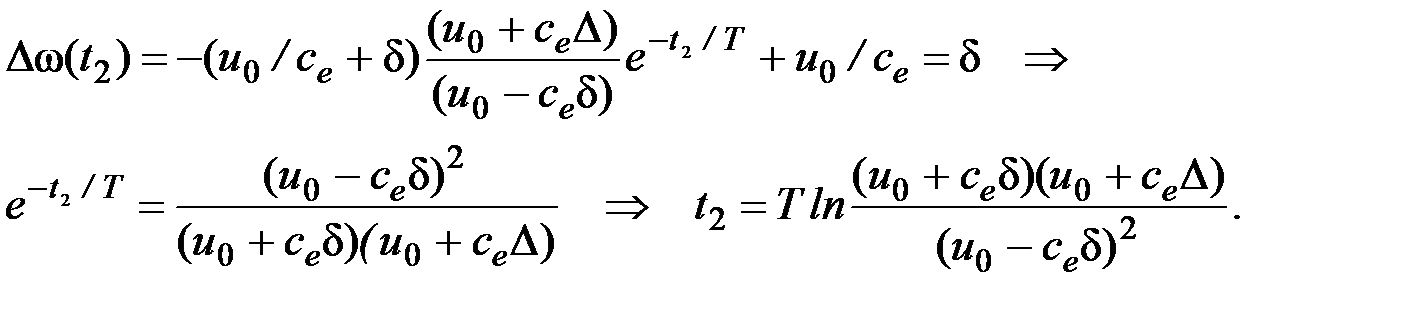
Если обозначить t = t 1 + t, где t – время после начала 2-го этапа, то 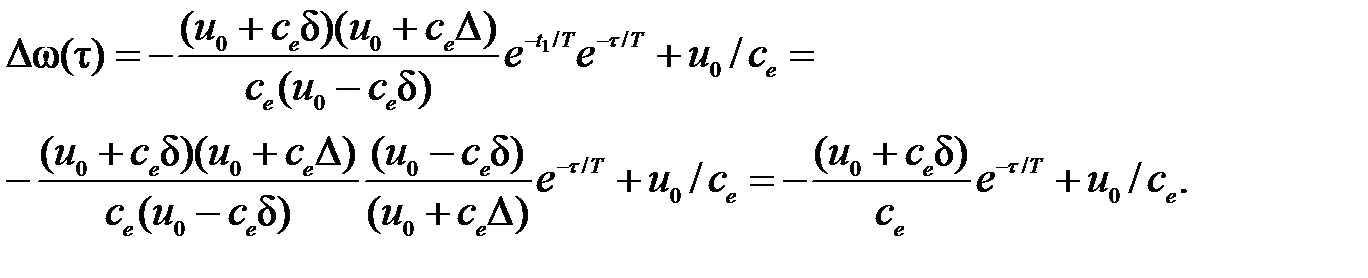
3-ий этап. Начинается в момент времени t = t 2, когда отклонение скорости двигателя Dw(t 2) достигло d. Поэтому, как и на 1-ом этапе, «двигаемся» по участку 4:

4-ый этап. Начинается в момент времени t = t 3, когда отклонение скорости двигателя Dw(t 2) достигло –d. Поэтому, как и на 2-ом этапе, «двигаемся» по участку 2:

Если обозначить t = t 3 + t, где t – время после начала 4-го этапа, то
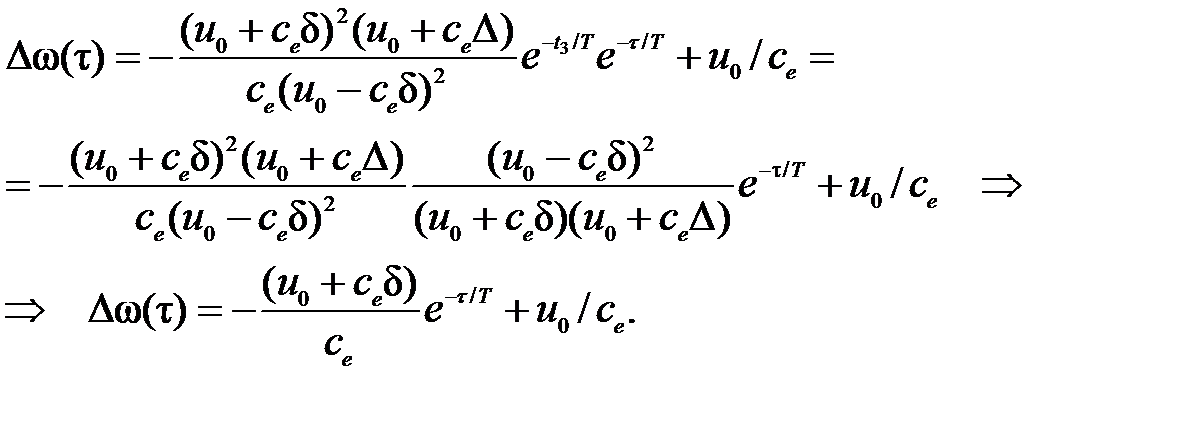
Выражения для Dw(t) на 2-ом и 4-ом этапах идентичны. Дальше все будет повторяться. Следовательно, в системе наблюдаются автоколебания (рис. 5.5).

| t |
| t4 |
| t2 |
Амплитуда автоколебаний равна d, т. е. определяется шириной петли гистерезиса. Период колебаний равен T a = t 3 – t 1.
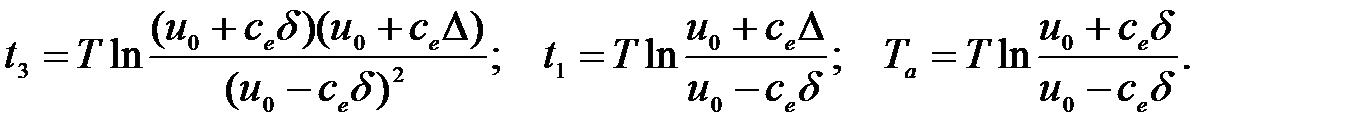
Поиск по сайту: