 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Управляемость и наблюдаемость объектов
Управляемость и наблюдаемость являются такими же важными свойствами объектов, как и их устойчивость. Термин управляемость означает возможность перевода объекта из любого начального состояния (режима работы) X (t 0) = X 0 в любое конечное состояние X (t к) = Xк за конечное время 
путем приложения допустимого управления U (t). Объект, обладающий указанным свойством, называется полностью управляемым. Оценка управляемости должна выполняться перед тем, как переходить к оптимизации управляемой системы. Дело в том, что для не полностью управляемого объекта такая задача может оказаться неразрешимой.
Термин наблюдаемость означает возможность определения начального состояния объекта X 0 по результатам наблюдений за его выходом Y (t) на конечном интервале 
. Объект, обладающий таким свойством, называется полностью наблюдаемым. Оценка наблюдаемости объекта должна предшествовать постановке задачи его идентификации, так как не полностью наблюдаемый объект не может быть идентифицирован.
Итак, управляемость объекта означает возможность достижения его любого состояния, а наблюдаемость – возможность определения состояния в любой момент.
Для оценки управляемости и наблюдаемости используются уравнения состояния и уравнение выхода объекта в их векторно-матричной форме
где X – вектор-столбец переменных состояния[1 ´n ]; Y – вектор-столбец выходных переменных [1 ´q ], q £ n; U – вектор-столбец управлений [1 ´ m ], m £ n;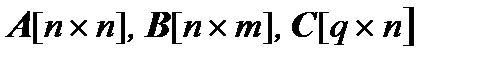 
– постоянные матрицы коэффициентов.
Система описывается n переменными состояния, q выходными переменными и m управляющими переменными.
Поиск по сайту: